プランクの放射法則
１．プランクの法則の解析解

物理学において、古典論では物理量であるエネルギーは連続的な値を許します。 それに対して、その後発展した量子論ではエネルギーが飛び飛びの値しか許さないという、不思議な制約が存在することが明らかになりました。 その発端となったのは、古典論では説明できなかった空洞放射の放射スペクトルの実験結果を説明するために、プランクによって導入されたエネルギー量子仮説です。空洞放射の放射スペクトルの温度依存性を示したのがプランクの法則として知られています。 （詳細は「黒体 - Wikipedia」をご覧ください。）

本稿は、プランクの放射法則を用いて有限サイズの完全導体中の電場の時間発展のシミュレーションを次のステップで行います。

１．プランクの法則の解析解
２．完全導体で囲まれた空洞における電磁波の基本モード
３．完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性
４．任意の温度に対する完全導体中の電磁波シミュレーション
本節は、出発点となるプランクの法則の解析解の概略を行います。

プランクの法則とは黒体放射において角振動数が にある電磁波の空間平均エネルギー密度を と表した場合、

(1)

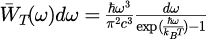
で与えられるという法則です。 式(1)は①各電磁波モードのエネルギーが離散的

(2)

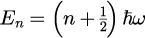
であり、②各電磁波モードの存在確率がカノニカル分布に従う

(3)

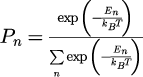
という条件から導出することができます。 下図は、式(1)の各振動数を波長に変換してプロットしたものです。 ただし、との関係は、です。

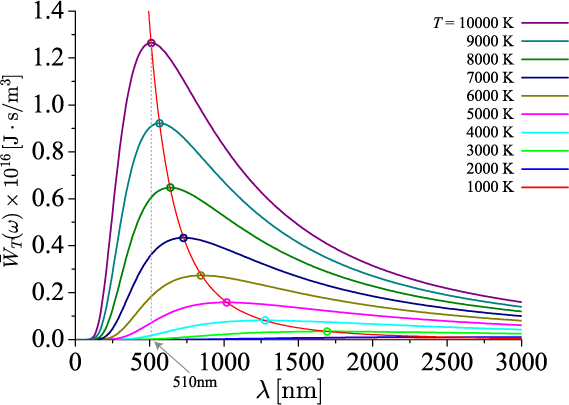
横軸に波長、縦軸に空間平均エネルギー密度とし、 各温度に対するスペクトルを表しています。 の最大値を与えるは式(1)から、

(4)

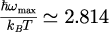
となり、対応する波長は

(5)

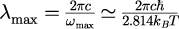
となります。では、およそで青緑の波長の光の強度が最大となります。 ちなみにの最大値を与える曲線（図中の赤線）は、

(4)

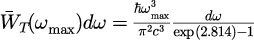
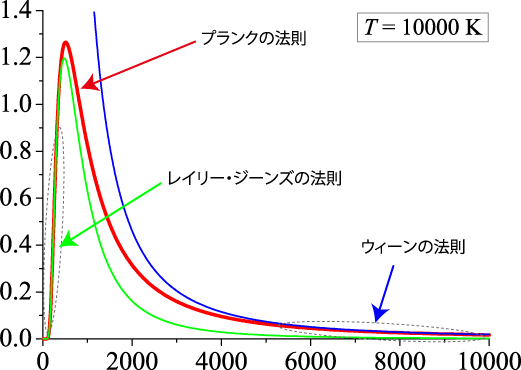
となります。歴史的には、プランクの法則が発見される前には、高温側のレイリー・ジーンズの法則、低温側は「ウィーンの法則」としてそれぞれ独立に発見されていました。 プランクの法則は、この２つの法則を包括していて、それぞれとの条件を用いて、式(1)を展開することで得られます。

レイリー・ジーンズの法則

(6)

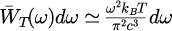
ウィーンの法則

(7)

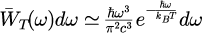
下図は、プランクの法則、レイリー・ジーンズの法則、ウィーンの法則をに対してプロットしたものです。