プランクの放射法則
２．完全導体で囲まれた空洞における電磁波の基本モード

量子力学の創成に重要な影響を与えたプランクの放射法則のシミュレーションを行います。
本稿では、完全導体で囲まれた真空中における電磁波の基本モードを用いた各種シミュレーションを次のステップで行います。
１．プランクの法則の解析解
２．完全導体で囲まれた空洞における電磁波の基本モード
３．完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性
４．任意の温度に対する完全導体中の電磁波シミュレーション

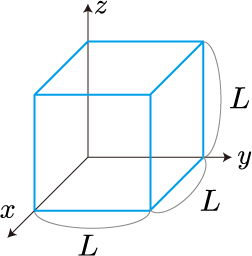
本節では、完全導体中の基本モードを導出します。その際のポイントは①境界条件と②電磁波の横波条件です。 次の図のように、長さの真空の立方体の周りが完全導体である系を考えます。

真空中の電磁波の電場は、マクスウェル方程式

(1)

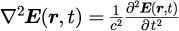
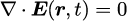
から、波数ベクトルを用いて

(2)

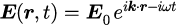
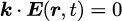
と表すことができます。電磁波の進行方向はとなるのに対して、の振幅の向きがの垂直方向となることがわかります。これは電磁波が横波であることを表しています。 この式(2)に完全導体との境界面における境界条件を課すことで、完全導体で囲まれた真空中における電磁波の基本モードを導出することができます。

①完全導体との境界面における境界条件

完全導体とは電気伝導度がの仮想の導体で、完全導体中では電場が０となります。 つまり、完全導体との境界面でとなる必要があります。 式(2)の実部に対して境界条件を課すと、

(3)

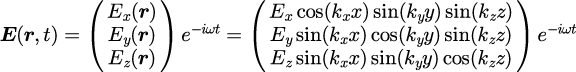
となります。 ただし、は

(4)

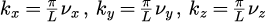
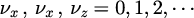
という制限がつきます。 ただし、は同時に２つ０になると電場は０になってしまうため、２つ以上０となるとはありません。 式(3)で与えられた電場に対する磁束密度はマクスウェル方程式の一つであるファラデーの電磁誘導の法則

(5)

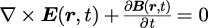
から、

(6)

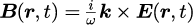
を計算することで得られ、

(7)

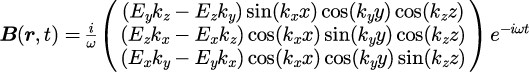
となります。 式(7)から、完全導体との境界面における磁束密度はとなることがわかります。 つまり、「【2-2】電磁波に対する透過係数と反射係数の導出」で触れたとおり、異なる媒質に対する磁束密度の境界条件が「磁束密度の境界面に対する垂直成分が連続」であることを考慮すると、電磁波が完全導体の内部には一切入り込まないことがわかります。

②波数ベクトルと電磁波の振幅に対する制限

次に、式(3)の電場の表式に電磁波が横波であるための条件を課します。 波数ベクトルは電磁波の進行方向を表すので、電場の振幅方向は波数ベクトルと垂直な面上にあるわけですが、電場の向きを直交する２つの方向に分解して考えます。

(8)

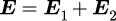
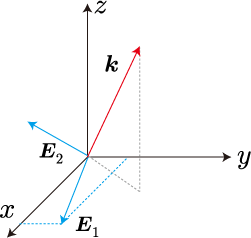
上の図は波数ベクトルと電場の向きとの関係を表しています。 波数ベクトルに対して、一つ目の電場の向きを

(9)

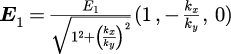
とxy平面とした場合、 ２つめの電場の向きは

(10)

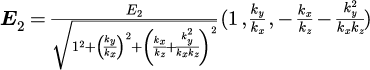
となります。 つまり、との各成分は独立ではなく、この２つのベクトルの和で表される電場だけであることがわかります。 本来x,y,z方向の３自由度に横波制限を課すことで電場の振幅に対する自由度は２となります。 ただし、式(9)と(10)の表式はの場合に成り立ちます。 の場合には、別途直交する２つの電場の方向を決める必要があります。

(11)

(12)

(13)

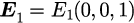
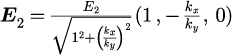
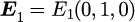
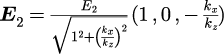
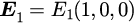
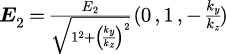
計算結果

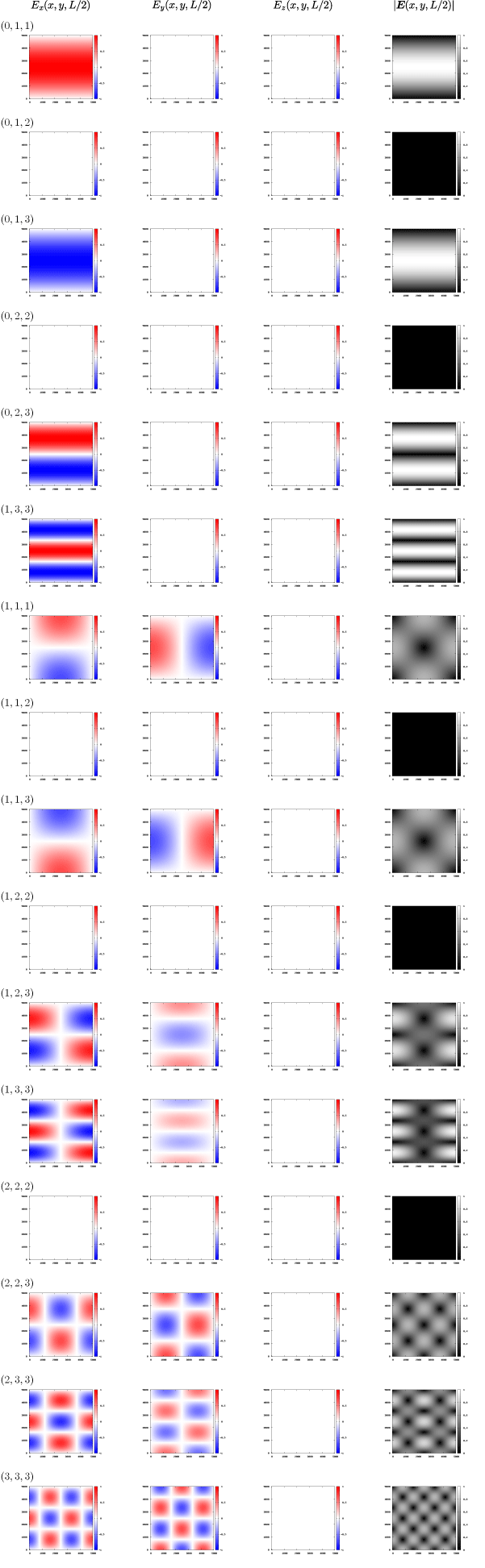
における電場モードを考えます。 グラフの横軸と縦軸のメモリは、赤と青は電場の最大値と最小値を表します。 の平面上における電場の空間強度分布を計算し、周期を20分割してアニメーションしています。

の電場空間分布

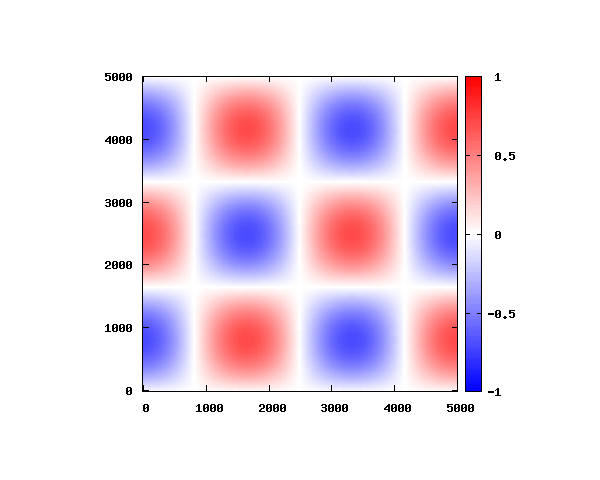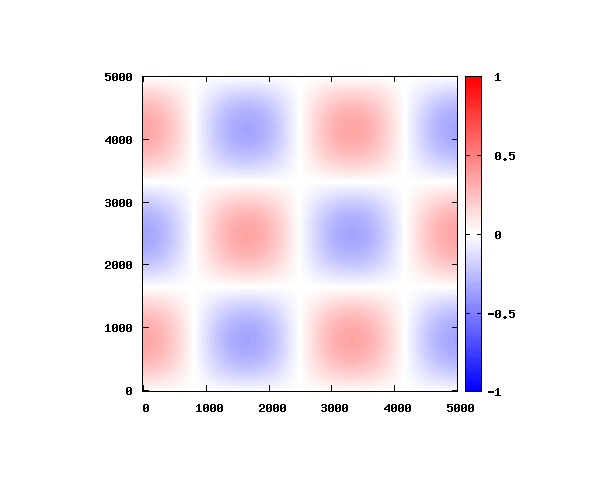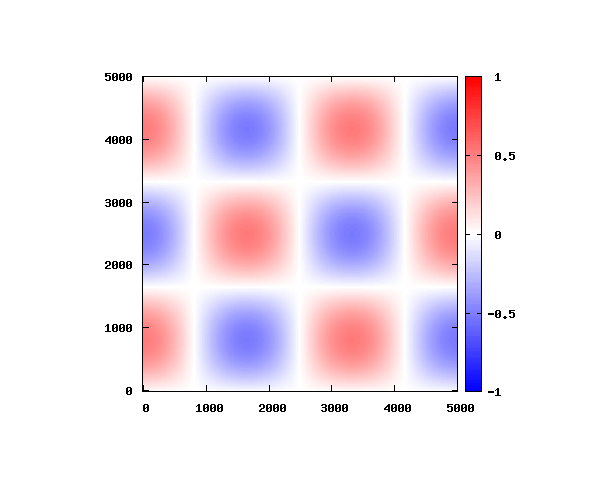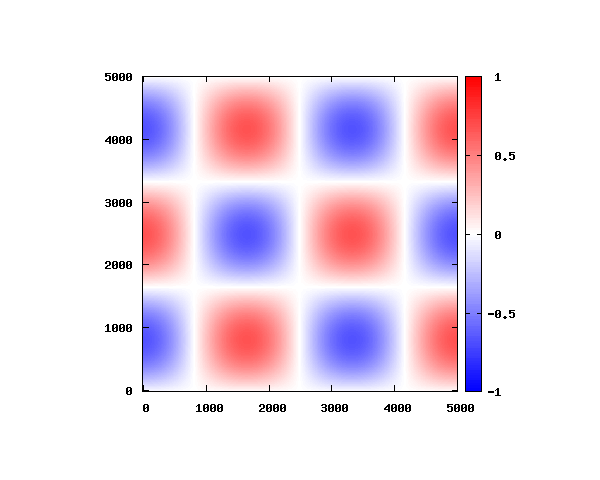
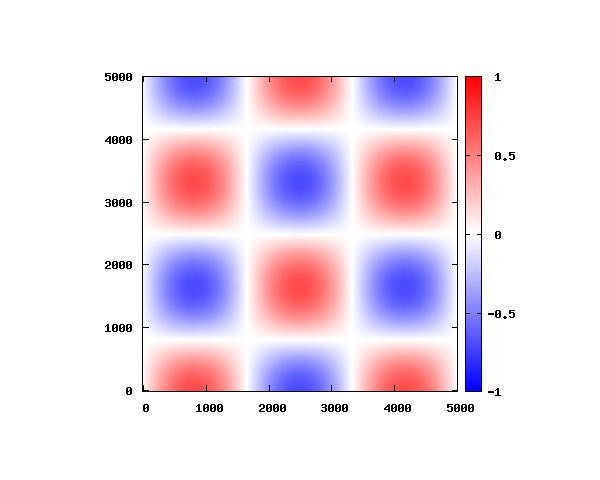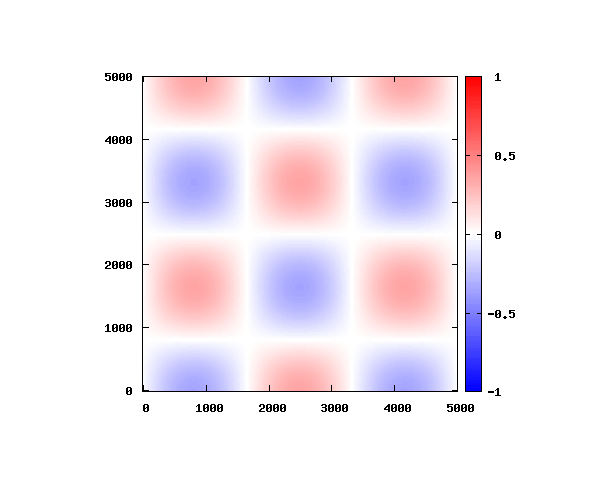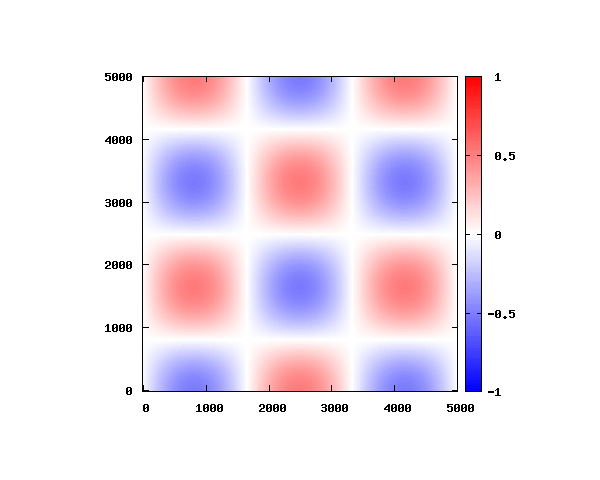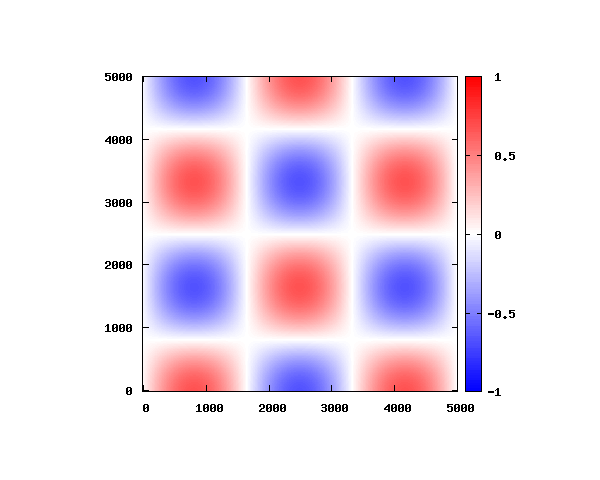
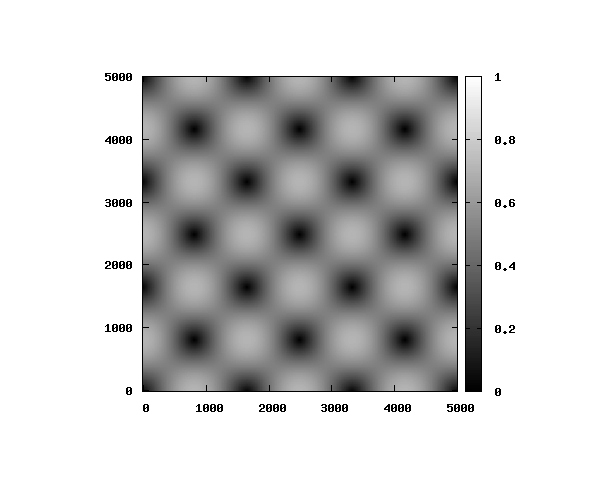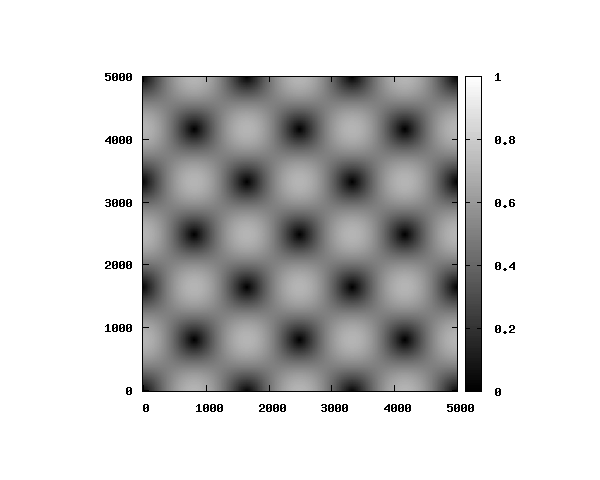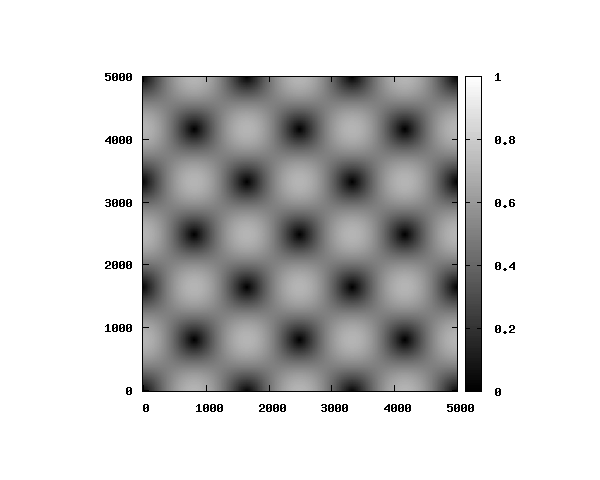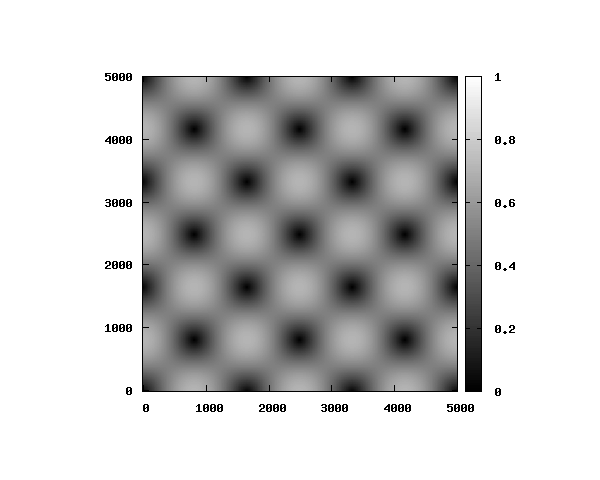
式(3)よりを代入すると、電場のz方向成分は０となります。 また、完全導体との境界面ではとなっていることがわかります。

電場モードの空間分布

最低モードは、 、 の３種類ありますが、対称性から全て同じ電場の空間分布を示します。 本節では重複を避けるために、最低モードからに従って計算結果を示します。