物性物理学入門
フォノン(格子振動)の分散関係(2原子)
前項では同じ質量とばね定数で結合された1列の原子に対する分散関係と運動を示しました。
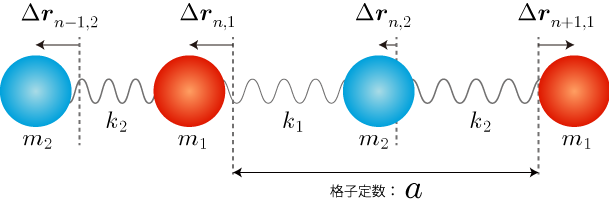
本項では下図のような2種類の質量とばね定数
で結合された1列の原子に対する分散関係のグラフを示します。
各原子の振動数を表す角振動数と、生成されるフォノン(格子振動)の波の数を表す波数
の間には次の関係があります。
は2種類の原子の振動に関する方程式から得られ、1原子の場合と異なり2次方程式の解として2つ存在します。
つまり、一つの波数
に対して、2つの角振動数
が存在することを意味します。この分散関係のグラフは次のとおりです。質量とばね定数を設定することができます。
2種類原子のフォノン分散関係
青色が、黄土色が
に対応し、それぞれ音響モード、光学モードと名前がついています。
2つのモードによる振動の違いを次に示します。なお、角振動数の最大値は
です。
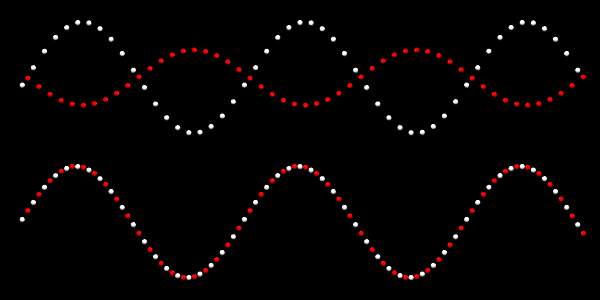
フォノンのスナップショット
下図は2種類の原子を間隔1(格子定数2)で並べて変位を上下で表した図です。波数(波長
)に対する光学モード(上段)と音響モード(下段)の表しています。
生成されるフォノンの波長は同じですが、2種類の原子配置が全く異なり、先述のとおり角振動数も異なります。 2つのモードの運動アニメーションはこちらです。
物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。