【物理シミュレーションに挑戦！】古典力学
様々な力による物理シミュレーション１：弾性力による運動

本項は物理学における様々な系の物理現象を、解析的に扱うのではなく数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・様々な力による物理シミュレーション１：弾性力による運動
・様々な力による物理シミュレーション２：万有引力による運動
・様々な力による物理シミュレーション３：クーロン力による運動
・様々な力による物理シミュレーション４：レナード・ジョーンズ相互作用による運動
・様々な力による物理シミュレーション５：引力＋衝突力

２点間の距離に比例した弾性力で運動する質点の運動は周期運動を行います。この周期運動は固有振動と呼ばれる基本的な振動の重ね合わせで表現することができます。 本項では、弾性力による質点運動シミュレーションするために必要な計算アルゴリズムを示します。

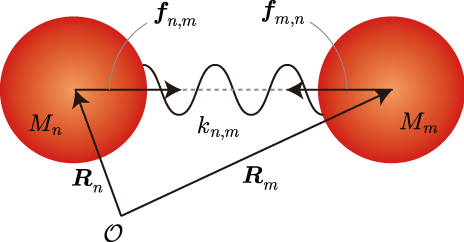
上図はn番目とm番目の２つの質点間を線形ばねで結合した模式図です。ばねによる弾性力 はバネ定数 を用いて

と表されます。もし、複数の質点と線形ばねで結合されている場合、n番目の質点に加わる力はそれらのばね弾性力を足し合わせた

で与えられます。そのため、n番目の質点の時間発展は運動方程式から

となります。

弾性力による質点運動シミュレーション

異なる質量の２つの質点

ばねが一つの場合、周期運動は質量とばね定数で与えられる固有振動運動となります。

異なる質量の３つの質点

結合数が３つの場合も周期的な運動を行います。本項では示しませんが、この周期的な運動は固有振動の重ね合わせで表現されます。

ばねに自然長が存在する場合

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。