【物理シミュレーションに挑戦！】古典力学
様々な力による物理シミュレーション２：万有引力による運動

本項は物理学における様々な系の物理現象を、解析的に扱うのではなく数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・様々な力による物理シミュレーション１：弾性力による運動
・様々な力による物理シミュレーション２：万有引力による運動
・様々な力による物理シミュレーション３：クーロン力による運動
・様々な力による物理シミュレーション４：レナード・ジョーンズ相互作用による運動
・様々な力による物理シミュレーション５：引力＋衝突力

質量をもつ２つの物体には万有引力と呼ばれる引力が働きます。 本項では、万有引力による質点運動シミュレーションするために必要な計算アルゴリズムを示します。

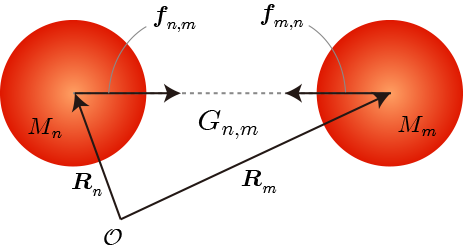
図は２つの質点間に働く万有引力の模式図です。万有引力は２つの質点の質量に比例し、２点間の距離の２乗に反比例し、力の向きは２点間を結ぶ直線上で引力として働きます。そのため、m番目の質点からn番目の質点に与えられる万有引力は

と与えられます。ただし、Gは万有引力定数と呼ばれる定数です。また、力の向きを与える単位ベクトル は

と定義します。もし、複数の質点が互いに万有引力を及ぼし合う場合、n番目の質点に加わる力は各万有引力を足し合わせた

で与えられます。そのため、n番目の質点の時間発展は運動方程式から

となります。

運動エネルギーとポテンシャルエネルギー

系全体の運動エネルギーとポテンシャルエネルギーはそれぞれ次のとおり与えられます。

両者の和系全体の運動エネルギー

は時間に依存しません。

万有引力運動シミュレーション

楕円運動を行う初期条件に対するシミュレーション結果です。万有引力を矢印で表しています。

３体問題

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。