１次元量子力学における調和振動子
任意の初期空間分布＋任意の中心運動量に対する時間発展

前節「１次元量子力学の調和振動子における任意の初期運動量分布＋任意の中心座標に対する時間発展」にて、本稿の目的である任意の初期状態に対する時間発展の計算手法を示すことができたわけですが、ここまでまとめている間にもっと簡単な方法に気が付きました。これまでの復習ついでに説明します。

任意の初期空間分布かつ中心運動量に対する時間発展を与える表式の導出

１．状態ベクトルを展開する

(1)

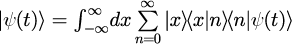
２．各因子にこれまでに得られている関数で表す

(2)

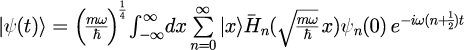
３．固有状態の座標表記

(3)

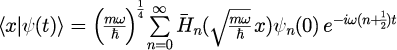
４．展開係数を与える表式

(4)

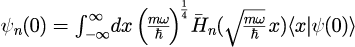
５．初期空間分布に虚数部を与えることで、中心運動量をにずらす

(5)

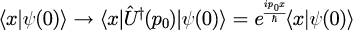
６．式(5)を式(4)に代入する

(6)

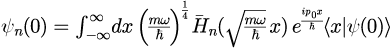
７．式(6)の初期空間分布をガウス分布とする

(7)

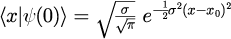
式(6)に式(7)を代入し、展開係数を得た後、式(3)に得たを代入して和をとることで時間発展を計算することができるという手順です。

式(5)の中心運動量を移動させる表式は、運動量平行移動演算子を用います。

運動量平行移動演算子

運動量平行移動演算子は

(8)

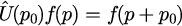
で定義されます。運動量表記による具体型は式(8)をテーラー展開することで

(9)

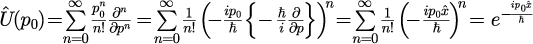
となり、通常の平行移動演算子と同様に表すことができます。 ただし、運動量表記における座標演算子はで与えられること用いています。

ガウス型運動量分布の時間発展

、、に対しての計算結果をアニメーション化したのが下図です。 図の横軸が 、縦軸が を表し、 赤線、緑線と青線は、それぞれ の実部、虚部と絶対値を表します。 アニメーションの時間間隔は、 です。

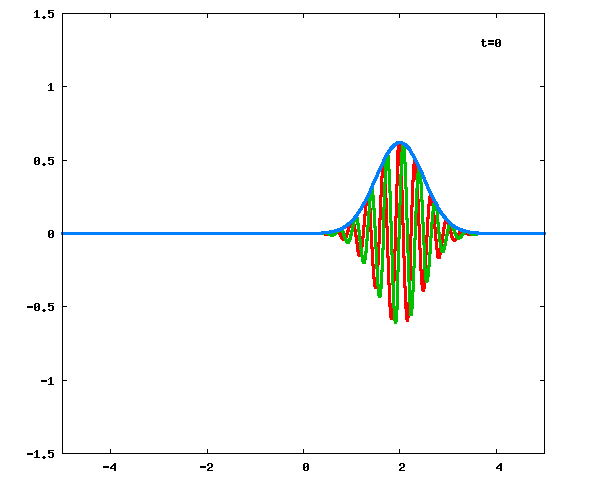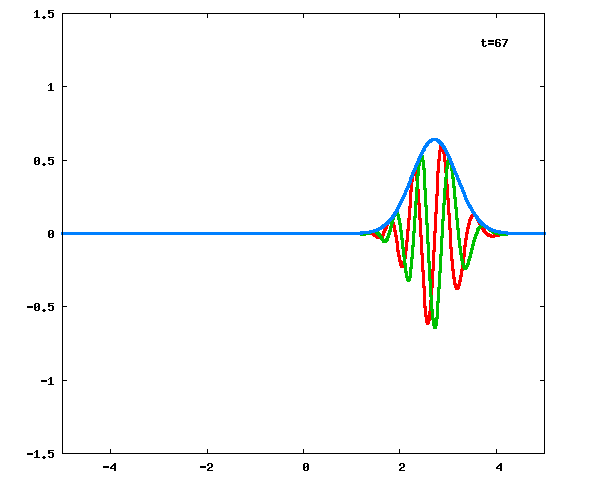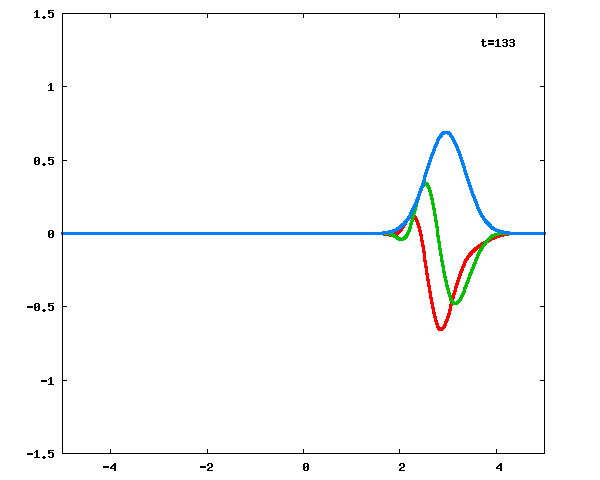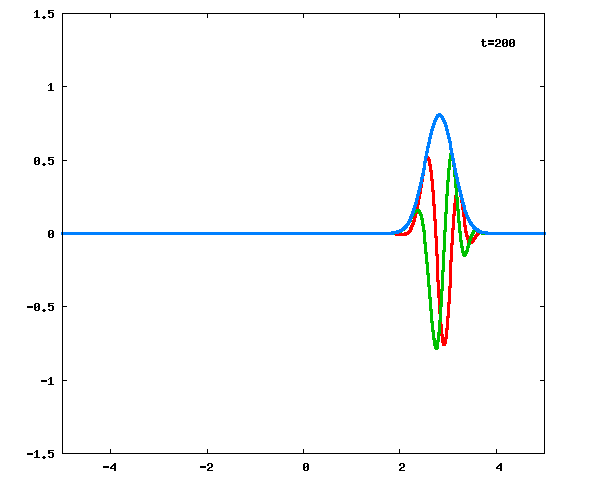
式(6)→式(3)で、意図通り計算することができました。

C言語プログラムソース

複素数を含んだ関数の多重積分については、 「シンプソン法を用いた複素数を含んだ２重積分(C++)」 をご覧ください。

/*
調和振動子の波動関数_任意の初期空間分布＋任意の中心運動量に対する時間発展
(2011.11.23 公開) */
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

const double PI = acos(-1.0);
const double e = 2.7182818284590452354;
const complex<double> I = complex<double>(0.0,1.0);
const double c = 2.99792458E+8;
const double lambda0 = 500.0E-9;
const double mu0 = 4.0*PI*1.0E-7;
const double epsilon0 = 1.0/(4.0*PI*c*c)*1.0E+7;
const double h  = 6.6260896 * 1.0E-34;
double hbar = h/(2.0*PI);
const double me = 9.10938215 * 1.0E-31;
const double eV = 1.60217733 * 1.0E-19;
int kizami = 3000;

double omega = 1.0 * 1.0E+15;
double sigma = 2.0 * 1.0E+9;
double x0 = 2.0 * 1.0E-9;
double p0 = 2.0 * 1.0E-24;

const int N_max = 300;//エルミート多項式の項数 
complex<double> Psi_n[N_max+1] = {0.0}; //エルミート多項式の係数

double A = sqrt(me*omega/hbar);
double dx = 1.0 * 1.0E-11;
double Dx = 1.0 * 1.0E-9;
const int ts = 0, te = 200;                   //<------------ステップ数を指定
double dt  = 1.0 * 1.0E-16;                   //<------------時間間隔を指定
//double dt= 2.0*PI/(E/hbar)/double(te-ts+1);    //<------------時間間隔を指定


int Lx = 1000;
string folder = "harmonic6";//作成するフォルダ名

//関数プロトタイプ
double NormalizedHermite( int n, double x );//規格化エルミート多項式
complex<double> Simpson(double a, double b, int n);

//被積分関数
complex<double> Integrand(double x, int n){ 
  return  sqrt(A) * NormalizedHermite(n, A*x) * exp(I*p0*x/hbar) * sqrt(sigma/sqrt(PI)) * exp(-1.0/2.0 * pow((sigma*(x-x0)),2)) ;
}

char str[200];
int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(11);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif

  string f1 = folder + "/Psi_n.data";
  ofstream ofs( f1.c_str() );
  for(int n=0; n<=N_max; n++){
    Psi_n[n] = Simpson( -Lx/2 * dx, Lx/2 * dx , n);
    ofs << n << " " << Psi_n[n].real() << " " << Psi_n[n].imag() << endl;
  }
    
  #pragma omp parallel
  {
    #pragma omp for //schedule(dynamic, 100)
    for(int tn=ts; tn<=te; tn++){
      double t_real = dt * double(tn);
      cout <<  tn << endl;
      char str[200];
      string str1;
      ofstream fout_s;
      sprintf(str, "/%d.data", tn); str1 = folder + str;
      fout_s.open(str1.c_str());

      for(int i=-Lx/2 ; i<=Lx/2 ;i++){
        double x = dx * double(i);
        complex<double> Psi = complex<double>(0.0,0.0);
        for(int n=0; n<=N_max; n++){
          Psi += sqrt(A) * Psi_n[n] * NormalizedHermite(n, A*x) * exp(-I* omega * ( n + 1.0/2.0)*t_real);
        }
        Psi = Psi/sqrt(A);
        fout_s << x/Dx << " " << Psi.real() <<" " << Psi.imag() << " " <<  abs(Psi) << endl;
      }
    }
  }

}
double NormalizedHermite( int n, double x )
{
  double y0, y1, y2;
  y0 = sqrt(1.0/sqrt(PI)) * exp(-pow(x,2)/2);
  if( n==0 ) return y0;
  y1 = sqrt(2.0/sqrt(PI)) * exp(-pow(x,2)/2) * x;
  if( n==1 ) return y1;
  for(int m = 2; m<=n; m++ ){
    y2 = sqrt(2.0/double(m)) * x * y1 - sqrt(double(m-1)/double(m)) * y0;
    y0 = y1;
    y1 = y2;
  }
  return y2;
}
complex<double> Simpson(double a, double b, int n)
{
  complex<double> ss1 =0.0;
  for(int i=1; i<=kizami/2-1; i++){
    double x = a + (b-a)/double(kizami) * double(2*i);
    ss1 += Integrand(x, n);
  }
  complex<double> ss2 =0.0;
  for(int i=1; i<=kizami/2; i++){
    double x = a + (b-a)/double(kizami) * double(2*i-1);
    ss2 += Integrand(x, n);
  }
  return (b-a)/(3.0*double(kizami)) * ( Integrand(a, n) + Integrand(b, n) + 2.0 * ss1 + 4.0 * ss2 );
}

ファイルたち

C言語プログラム

■１次元調和振動子における任意の初期運動量分布に対する時間発展

gnuplotテンプレート

■Harmonic1_1D.plt
■Harmonic1_1D-1.plt

Illustrator

■１次元調和振動子における任意の初期運動量分布に対する時間発展