１次元量子力学における調和振動子
単一エネルギーの時間発展

準備

はじめに、量子力学における調和振動子に対する定常状態を簡単に整理します。 シュレディンガー描像における状態ベクトル

(1)

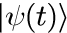
は、シュレディンガー方程式

(2)

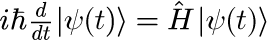
を満たします。 Hはハミルトニアンと呼ばれ、物理学におけるエネルギーに対応する物理量で、量子力学では演算子の形式を取ります。 式(2)を満たす状態ベクトル（式(1)）は、ハミルトニアン H の固有状態となり、固有値がエネルギー E となります。 式(1)の状態ベクトルは、ヒルベルト空間と呼ばれる無限次元空間に張られるベクトル量で、 後述のしますが、様々なベクトルとの内積を取ることで対象とする物理量を得ることができます。

１次元調和振動子の場合、ハミルトニアンは

(3)

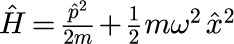
で与えられます。第１項は運動エネルギー、第２項はポテンシャルエネルギーを表す項です。 ポテンシャル項の m は粒子の質量、ωは角振動数です。 古典力学における運動量 p と位置 x は、p と x の積が順序に依らない c-数（classical number）と呼ばれる普通の数であるのに対して、 量子力学における p と x は共に演算子で表される q-数と呼ばれる量で、２つの数の積が積の順番に依存することです（非可換）。 さらに、運動量演算子 p と位置演算子 x に対応する固有ベクトルと固有値をそれぞれ定義することができます。

(4)

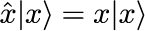
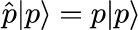
運動量演算子と位置演算子の固有値 x と p は c-数となることに注意が必要です。 運動量演算子と位置演算子に対する固有ベクトルは、式(1)の状態ベクトルから運動量情報および位置情報を取り出すことができるため、非常に重要です。 具体的には、式(1)の状態ベクトルと、運動量の固有ベクトルおよび位置の固有ベクトルとそれぞれ内積を取ることで、運動量表記および位置表記の波動関数を得ることができます。

(5)

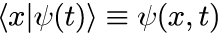
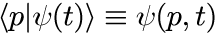
式(5)の２式の右辺が波動関数と呼ばれ、式(2)の方程式を満たす状態ベクトルに対して、運動量および位置の分布の時間依存性を表す表式となります。 波動関数は c-数です。座標表示による波動関数は特によく利用され、本稿でももっぱら座標表示を活用します。

量子力学における１次元調和振動子のハミルトニアン H は、個数演算子と呼ばれる運動量演算子 p と位置演算子 x を組み合わせて作られる演算子を用いることで調和振動子の本質を理解できます。個数演算子 N を用いるとハミルトニアン H は

(6)

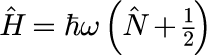
と表すことができます。運動量演算子や位置演算子と同様、個数演算子 N も対応する固有ベクトルや固有値が存在し、

(7)

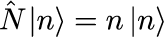
と表すことができます。|n> と n はそれぞれ個数演算子 N の固有ベクトルと固有値です。 個数演算子 N の固有値 n は正の整数です。 式(6)のハミルトニアンは個数演算子だけでできているので、個数演算子の固有ベクトル |n> は ハミルトニアンの固有ベクトルとなっていることがわかります。 つまり、ハミルトニアンを |n>に作用させると、

(8)

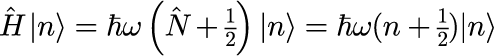
となり、ハミルトニアンの固有値、つまりエネルギーが得られます。 これは個数演算子 N の固有ベクトルは状態ベクトルのエネルギーを表していることがわかり、 固有値 n は正の整数をとるため、n=0 がエネルギーの最小値を与えることになります。

また、個数演算子 N の固有ベクトルも運動量演算子や位置演算子の固有ベクトルと同様、 状態ベクトルと内積を取ることで状態の個数表記の波動関数

(9)

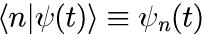
を得ることもできます。 運動量演算子、位置演算子、位置演算子の固有ベクトル、固有値に共通する重要な性質が３つあります。

１つ目は、異なる固有値を持つ固有ベクトル同士の内積が直交する正規直交性です。

(10)

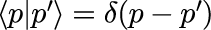
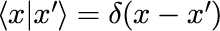
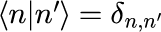
２つ目は、任意の状態ベクトルが固有ベクトルで張られるヒルベルト空間上で表現できる完全性です。

(11)

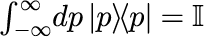
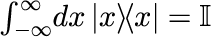
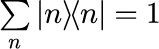
と表現されます。右辺の I は単位ベクトルです。

３つ目は、それぞれの演算子に対する固有値が実数となることです。つまり、x, p, n は実数（n は整数）となります。 上記３つの性質が成り立つための必要十分条件は演算子がエルミート演算子であることです。 物理量の実測値は実数であるため、物理量に対応する演算子は必ずエルミート演算子となり、固有ベクトルは上記の正規直交性と完全性を満たすことになります。

演算子に対応する固有ベクトルは式(5)や式(7)のような状態ベクトルとの内積だけではなく、 運動量演算子、位置演算子、位置演算子の固有ベクトル同士内積を取ることも出来ます。 特に重要なのは、個数演算子と位置演算子の固有ベクトル同士の内積で、

(12)

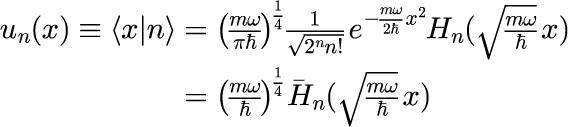
で与えられます。H_n はエルミート多項式と呼ばれる n 次の多項式で、ある微分方程式の一般解として与えられます。 （エルミート多項式の詳細については、
・エルミート多項式の直交性を確かめる
・エルミート多項式の規格化
をご覧いただければと思います。）

量子力学における１次調和振動子の時間発展を与える一般表式

ここまでで１次調和振動子の時間発展を与える一般表式を導出します。 はじめに、状態ベクトルを個数演算子の固有ベクトル |n> の完全性を利用して展開します。

(13)

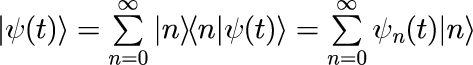
式(2)のシュレディンガー方程式に、式(13)と(6)を代入し左辺に移行し整理すると、

(14)

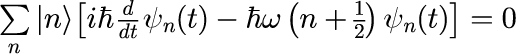
となります。 任意の個数演算子の固有ベクトルに対して式(14)が成り立つためには、[]の中が絶えず 0 である必要があります。 これは、時間 t に関する１階の微分方程式となるため、解は

(15)

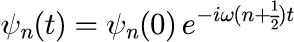
と直ちに得られます。１階の微分方程式なので積分定数が１つとなり、これが自由度となります。 具体的には、式(15)の右辺の係数 ψ_n(0)が n に対して任意で、状態の初期条件で一意に決まることになります。 式(15)を式(13)に代入した

(16)

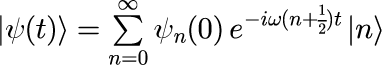
が、１次元調和振動子における状態ベクトルの時間発展を与える一般表式となります。 式(16)の状態ベクトルの位置表式における波動関数は、式(16)の両辺で位置演算子の固有ベクトルで内積をとる（両辺に左から <x|を掛ける）ことで得られ、 式(12)を代入することで

(16)

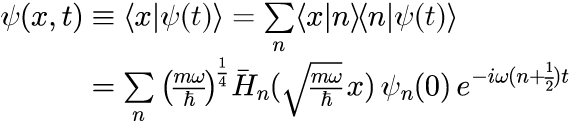
となります。式(16)は、１次元調和振動子における位置表記における波動関数のの時間発展を与える一般表式となります。 先にも触れましたが、ψ_n(0)は n に対して任意で初期条件で一意に決まるのですが、逆に言えば、 どんな ψ_n(0) の値に対しても式(16)は正しい時間発展を与えることになります。 これは、次節で行う「１次元量子力学における調和振動子における任意の初期状態に対する時間発展」で中心的役割を果たします。

１次元調和振動子に対する単一エネルギー状態の波動関数の時間発展

本節では、最も単純な単一エネルギー状態に対する位置表記の波動関数の時間発展を考えます。 そのためには、波動関数を単一の n となればよいので、ψ_n(0)を

(17)

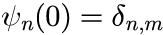
とすることで実現することができます。n の和を取り m→n とすると、 単一エネルギー状態の波動関数の時間発展を表す表式は

(18)

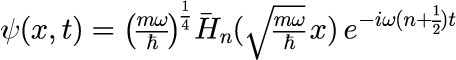
となります。計算するのためのパラメータは、電子を想定してエネルギーが eV 程度になるように設定します。

(19)

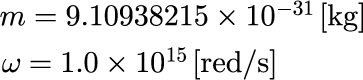
計算結果

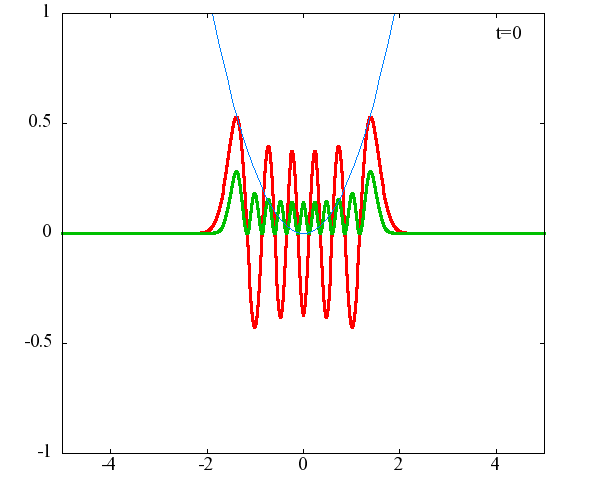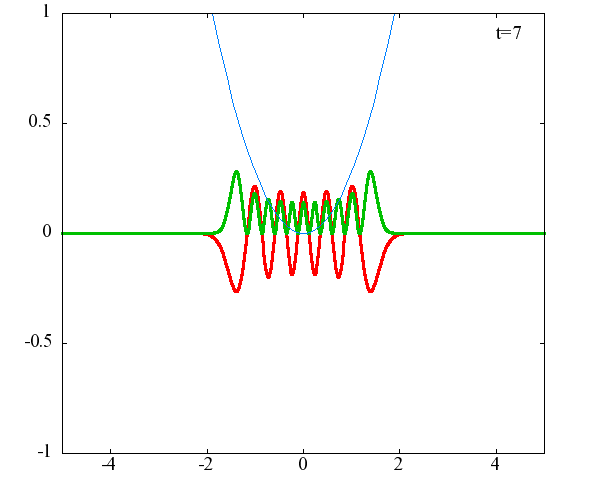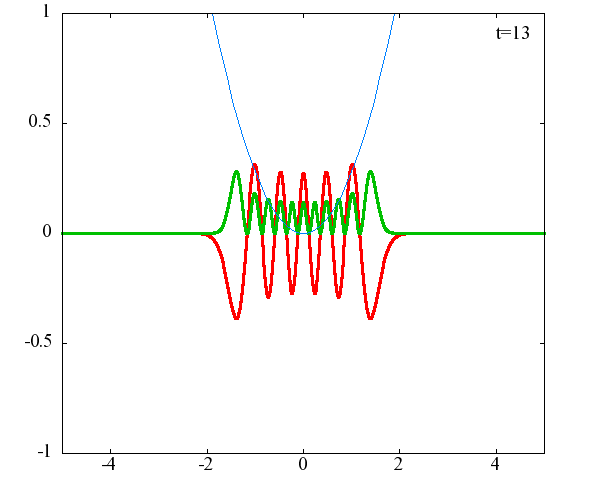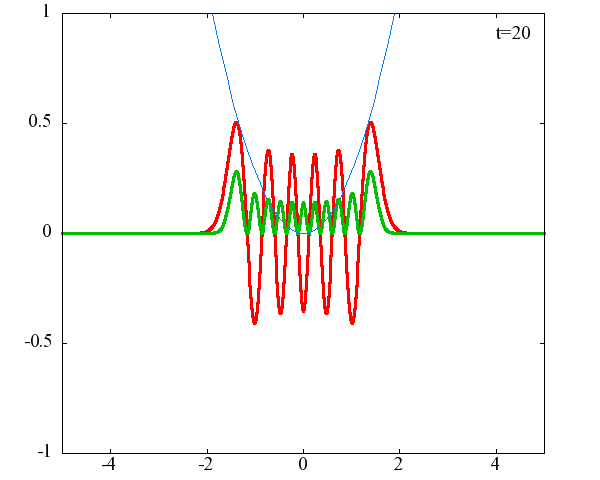
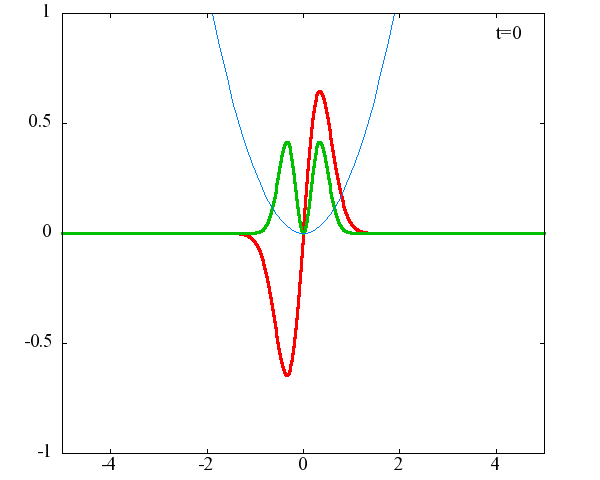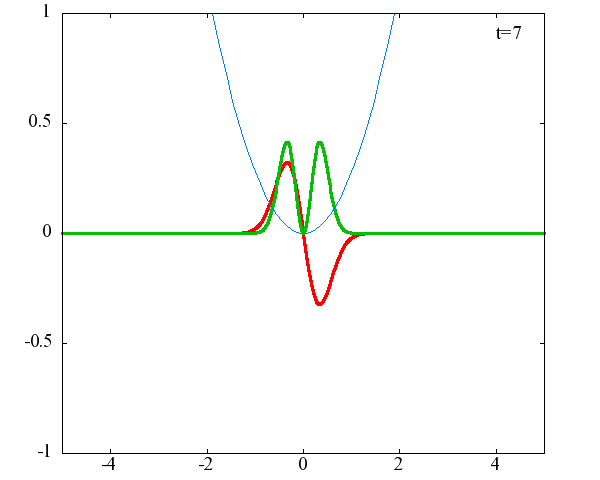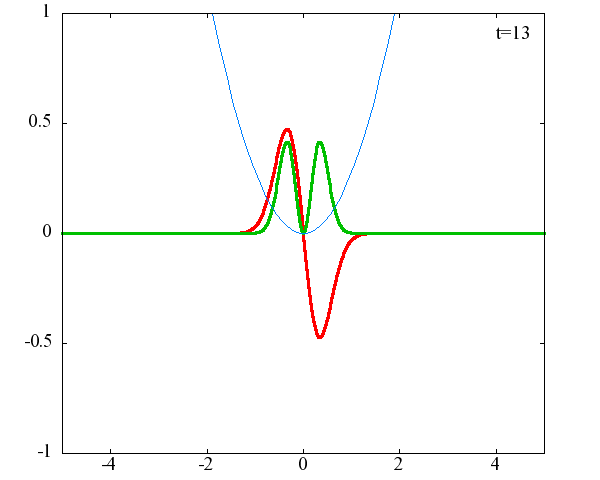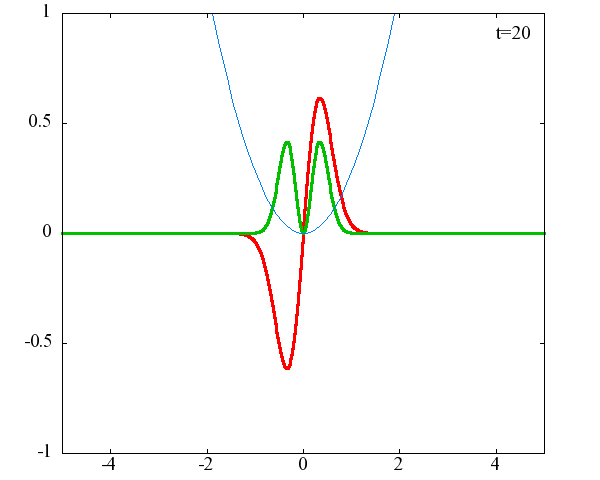
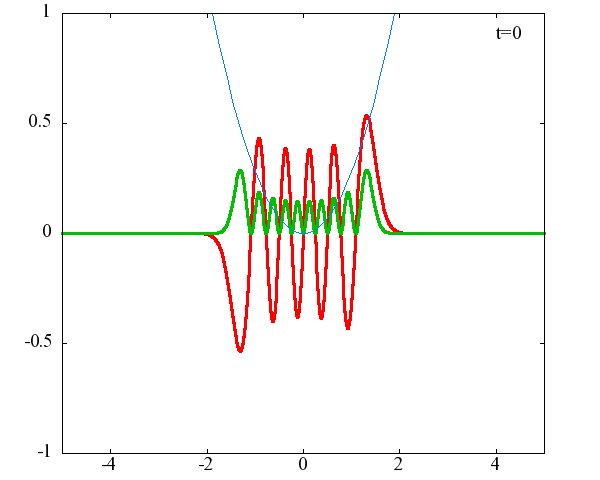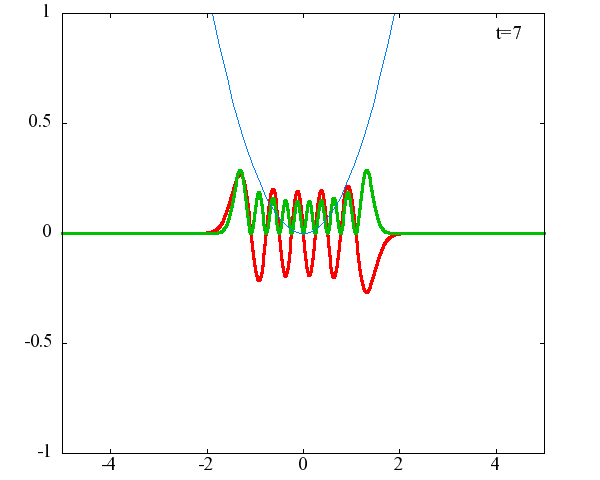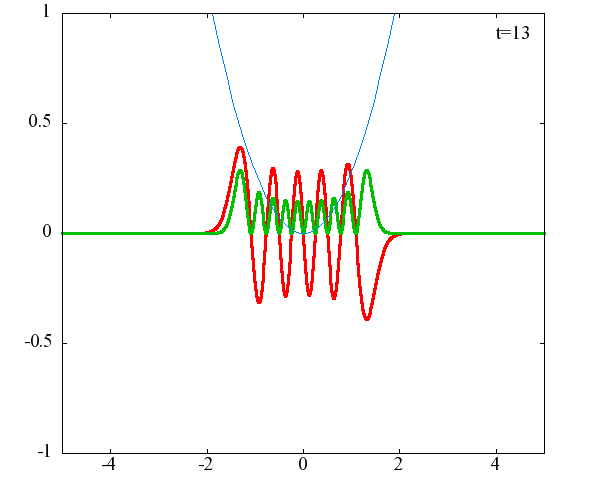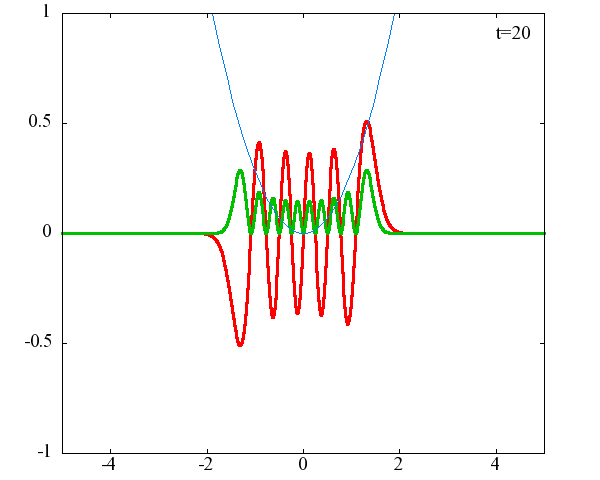
調和振動子の波動関数_単一エネルギーの時間発展にて計算しています。 単一エネルギーの場合、波動関数は時間に対して周期的になるので、周期を20等分して描画しています。 つまり、各 n に対する時間間隔は Δt=(2π/ω(n+1/2))/20 ～ 10^{16}[s]で、n ごとに時間間隔が異なることとに注意が必要です。 また、x 座標の単位は 1[nm] ( = 10^{-9}[m]) です。 なお、グラフの赤線は波動関数の実部、緑線は波動関数の絶対値の二乗です。

n=0


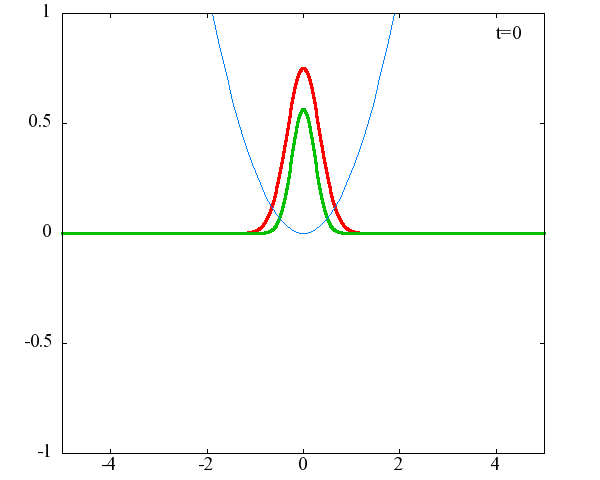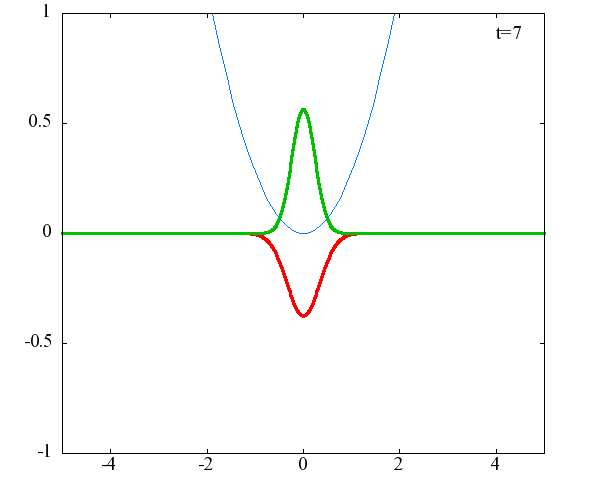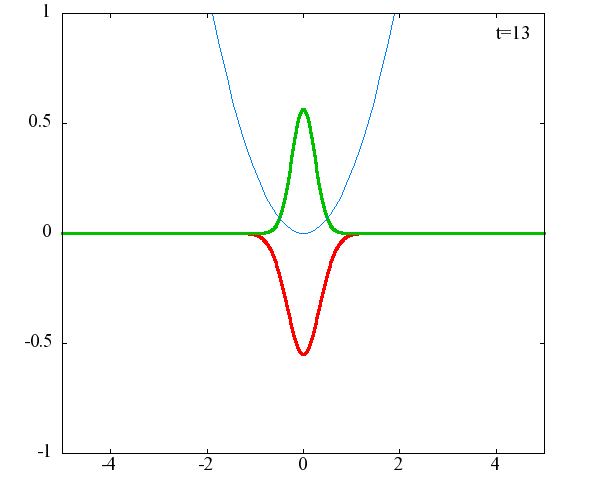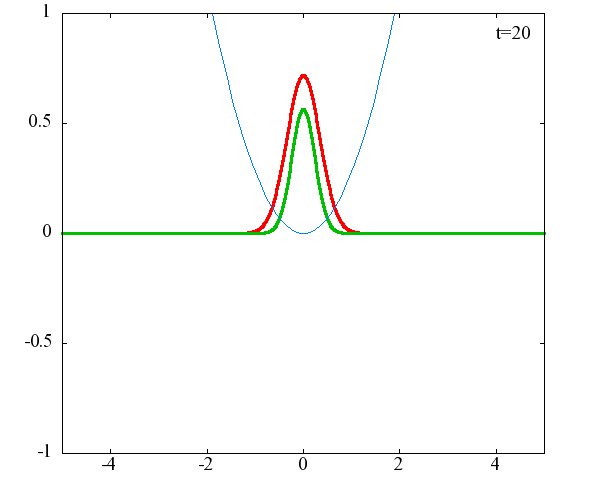
n=1


n=2


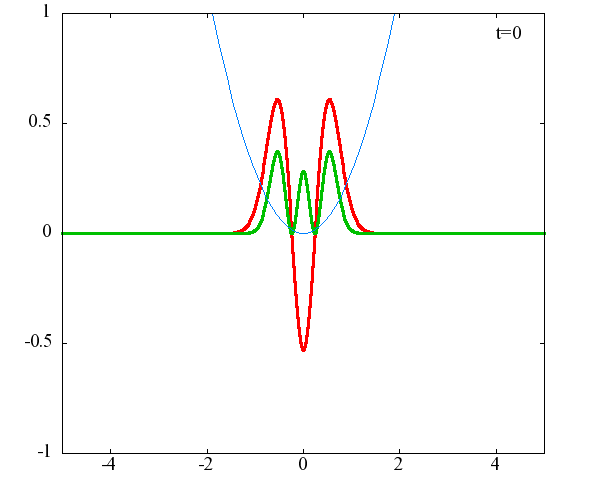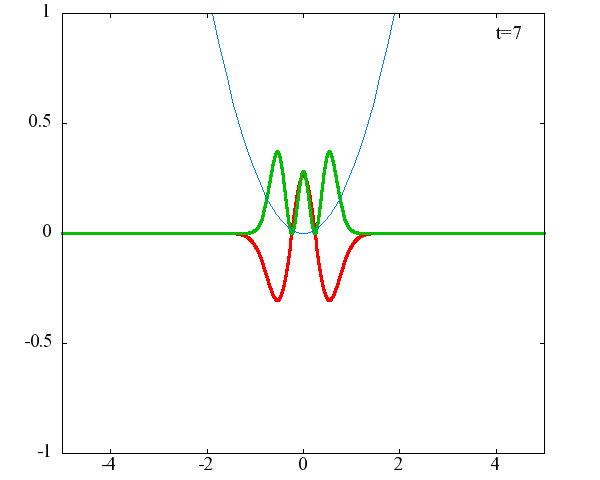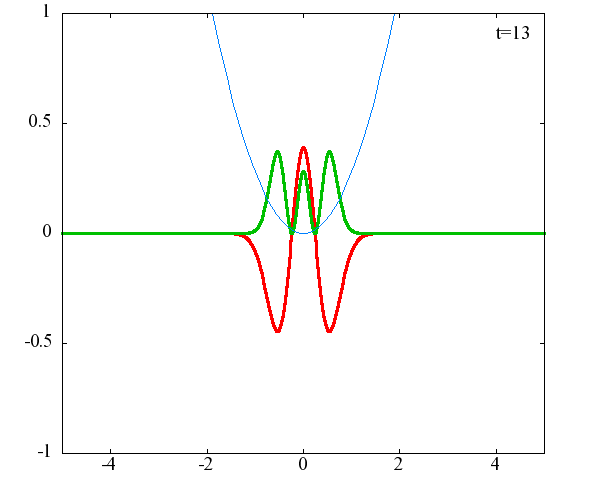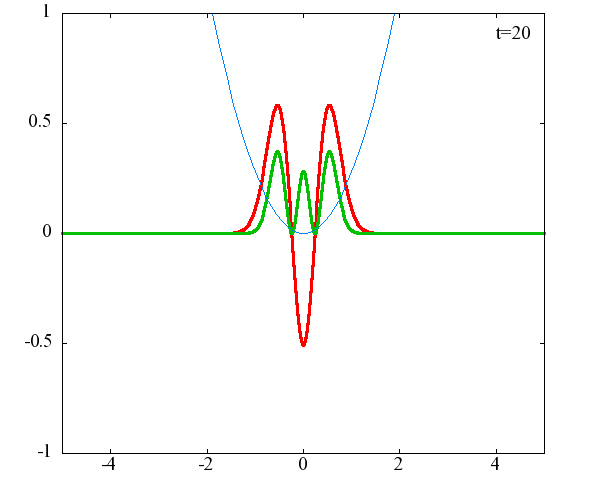
n=3


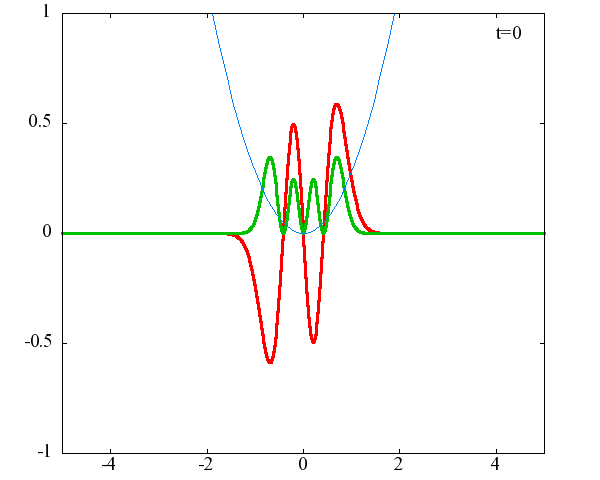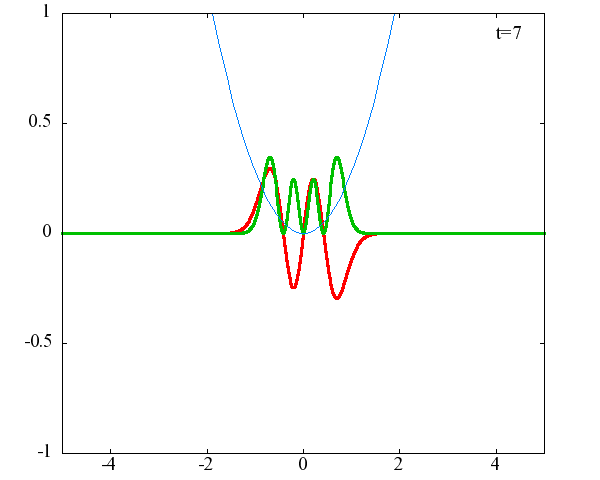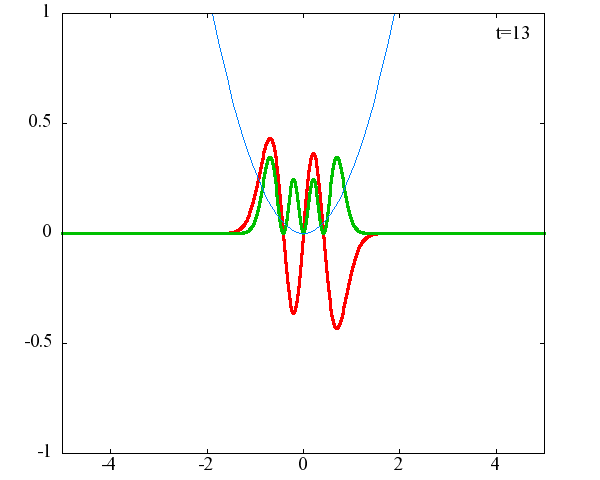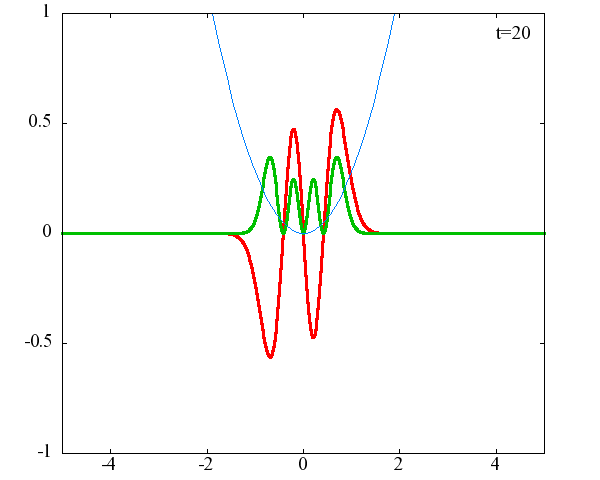
n=4


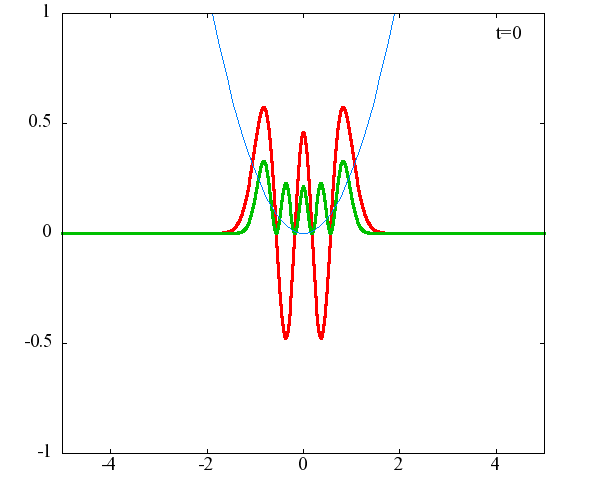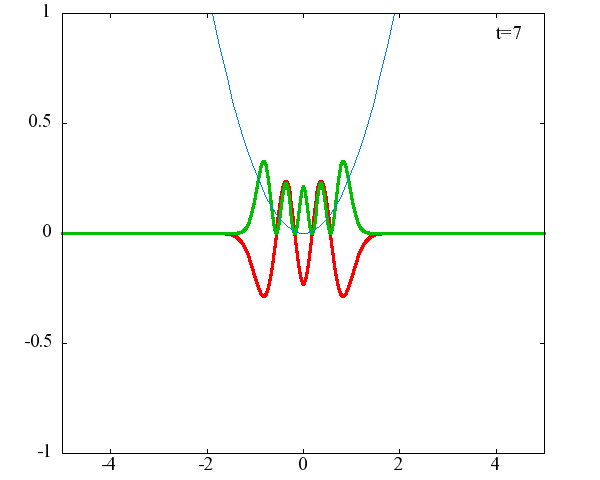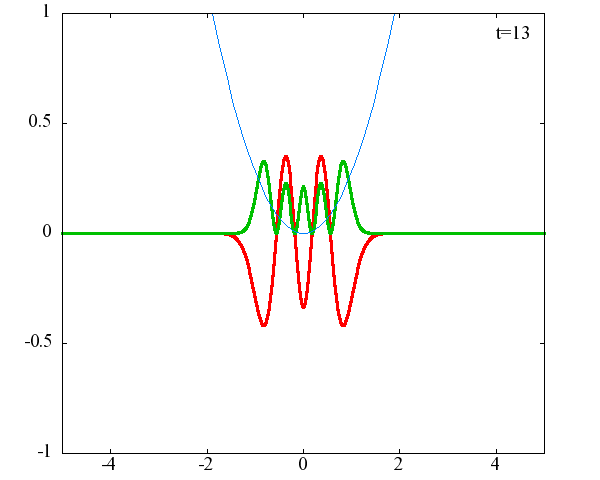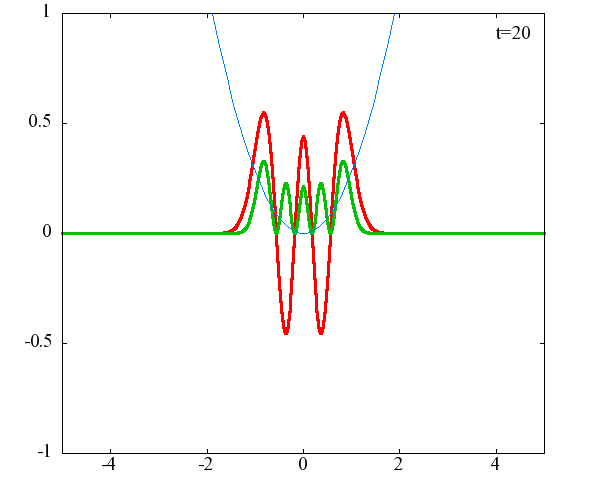
n=5


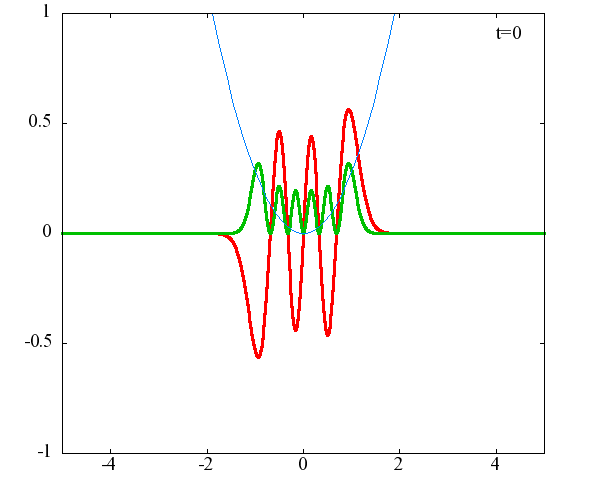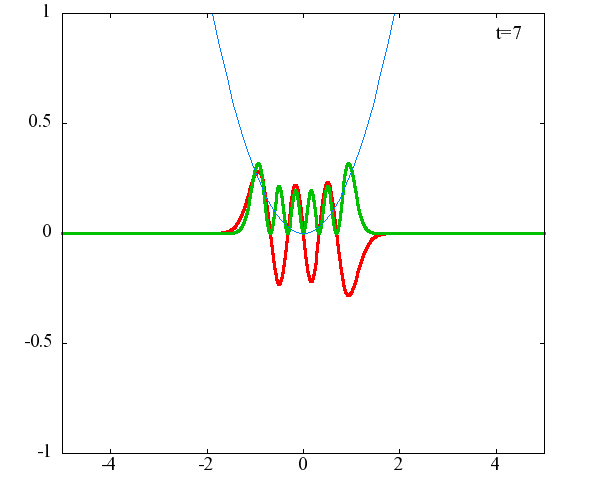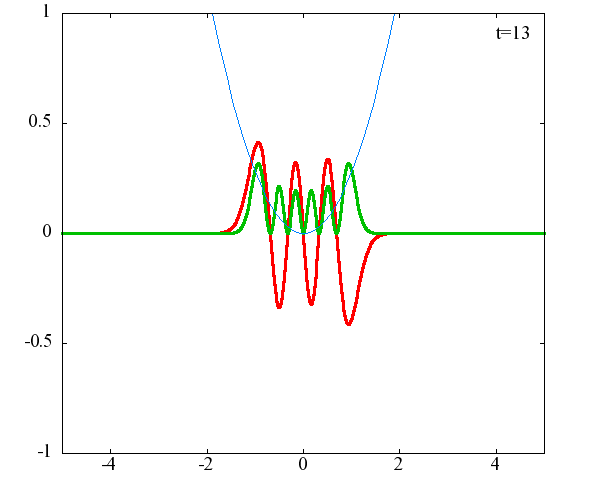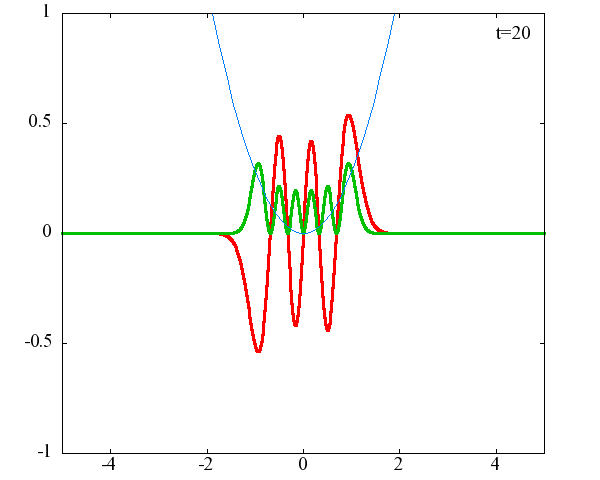
n=6


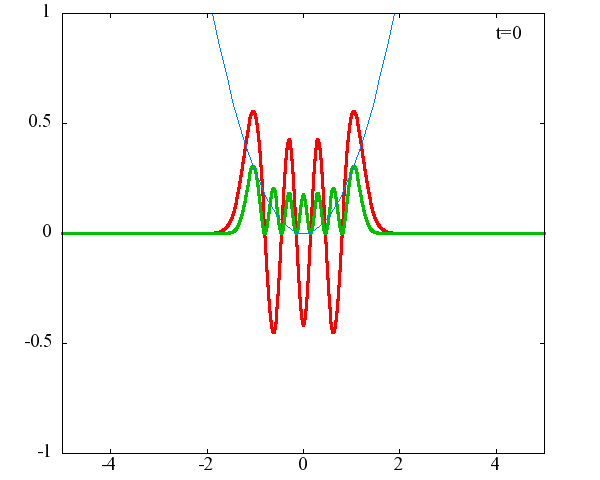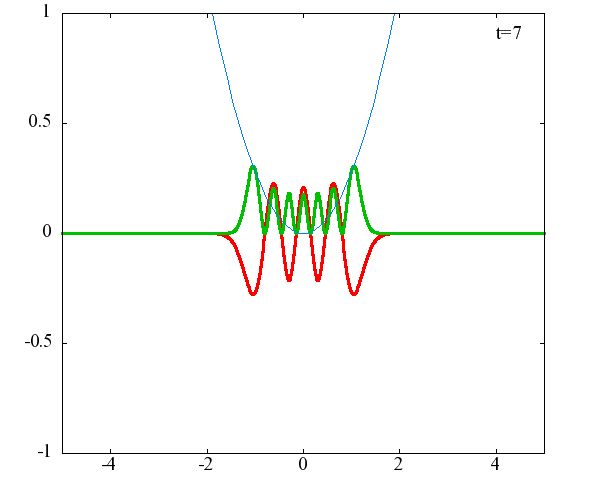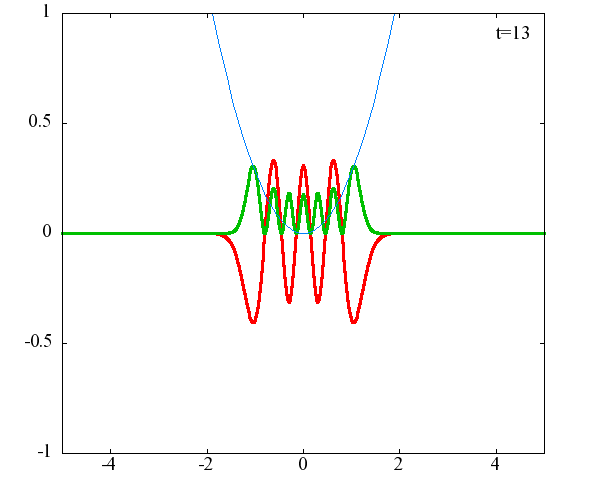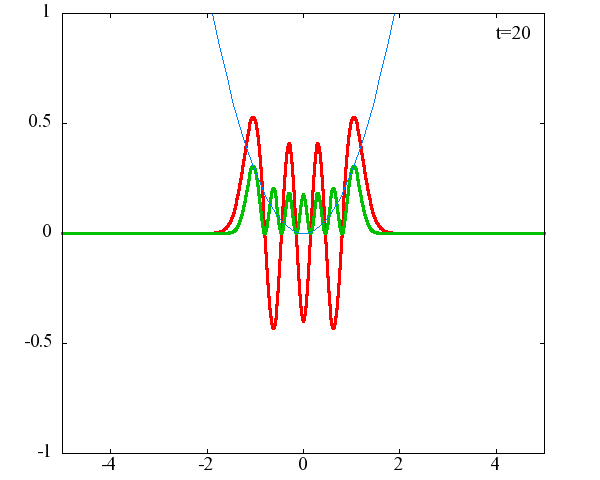
n=7


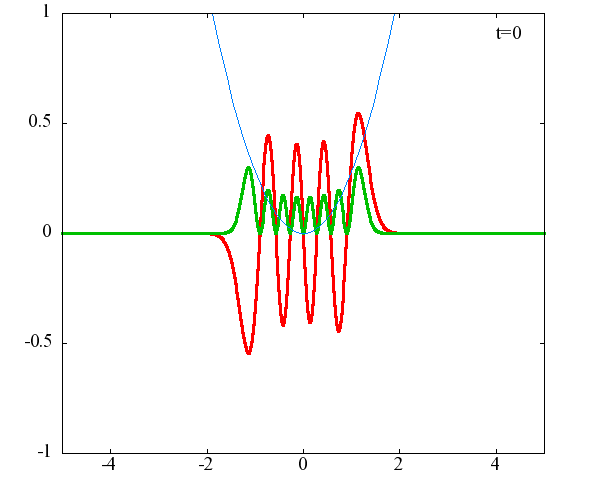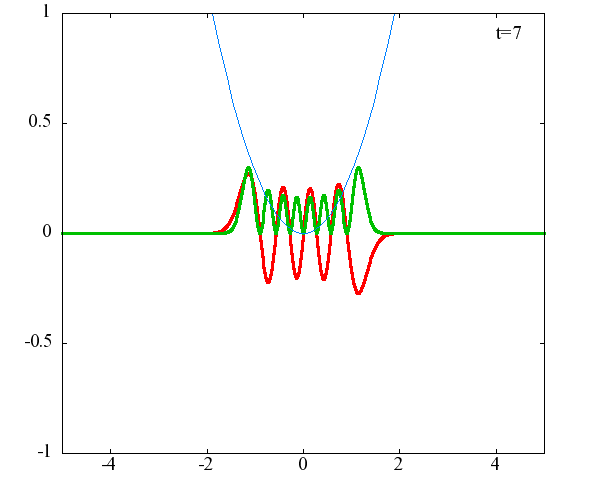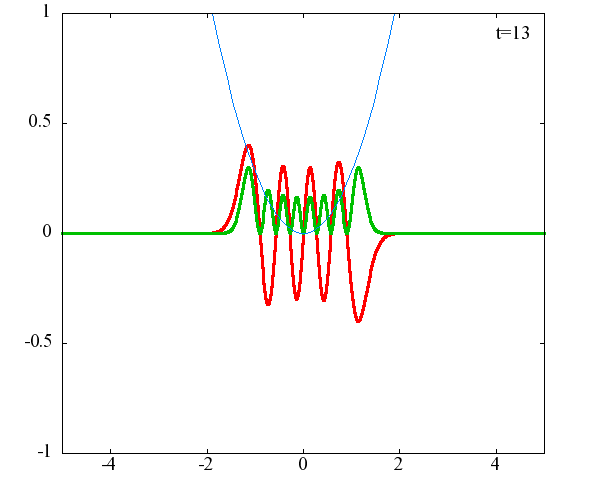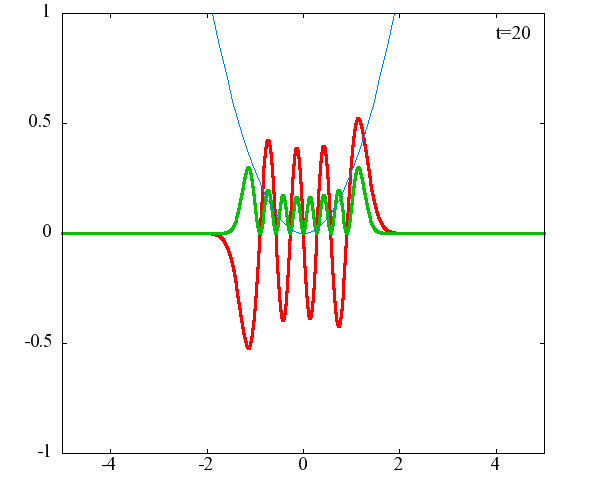
n=8


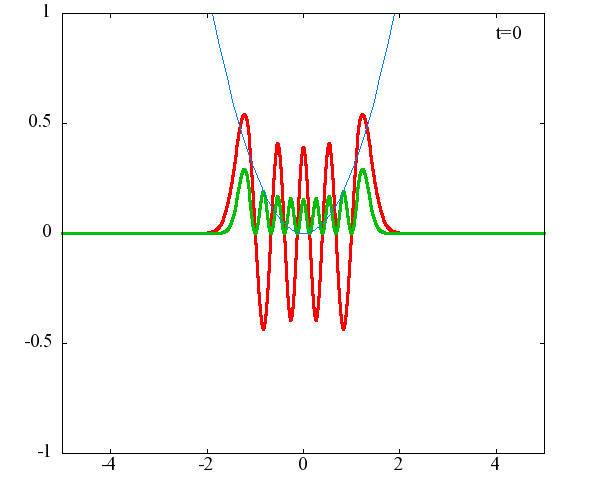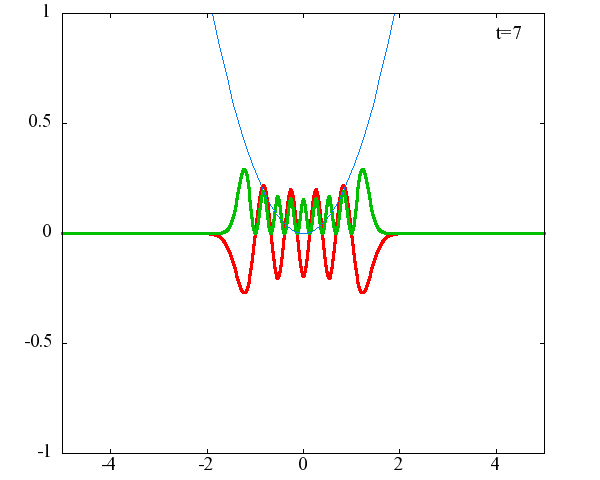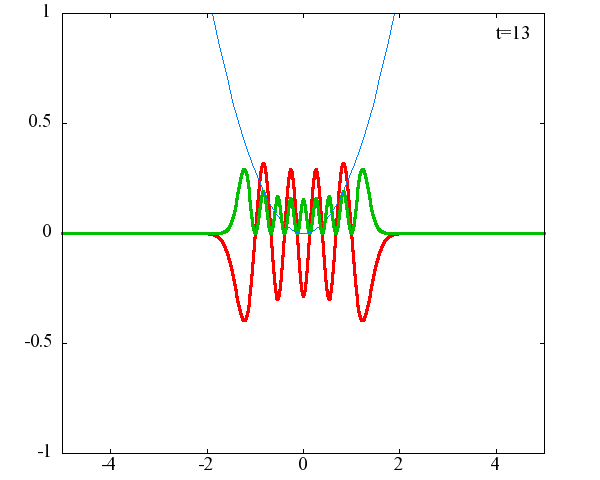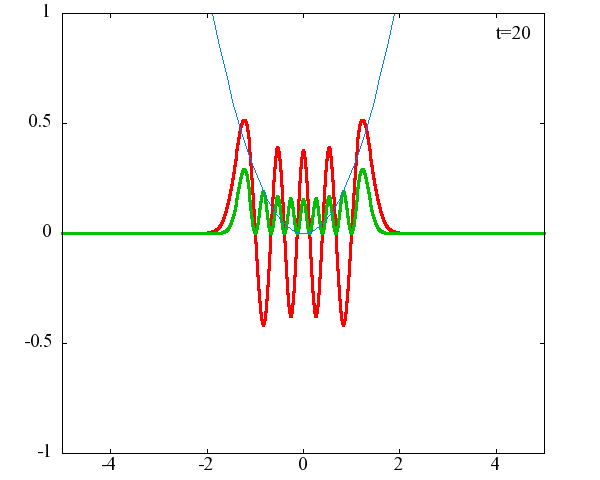
n=9


n=10