１次元量子力学における調和振動子
コヒーレント状態の空間分布

本節では、調和振動子におけるコヒーレント状態の時間発展を計算する準備として、コヒーレント状態の空間分布について考察します。 コヒーレント状態とは最小不確定性状態の一つで、調和振動子においては、 消滅演算子 a の固有ベクトルとして実現できることが知られています。 つまり、消滅演算子 a の固有ベクトルを |v>、固有値を v とした場合、

(1)

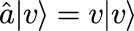
と表すことができます。消滅演算子はエルミート演算子ではないので v は複素数となります。 また、|v>は、個数演算子 N の固有ベクトル |n>を用いて、

(2)

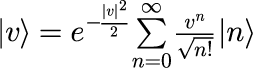
と展開できることが知られています。 話はそれますが、左辺から<n'| を掛けて、n と n' の直交性を利用することで、右辺の和が消えて、n' → n と置き直すと

(3)

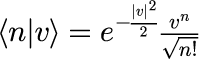
となります。式(3)はコヒーレント状態の個数表記となります。 つまり、式(3)の絶対値の２乗

(4)

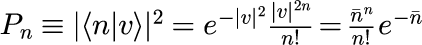
は、コヒーレント状態の個数 n に対する分布を表します。 ただし、bar{n} は、

(5)

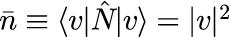
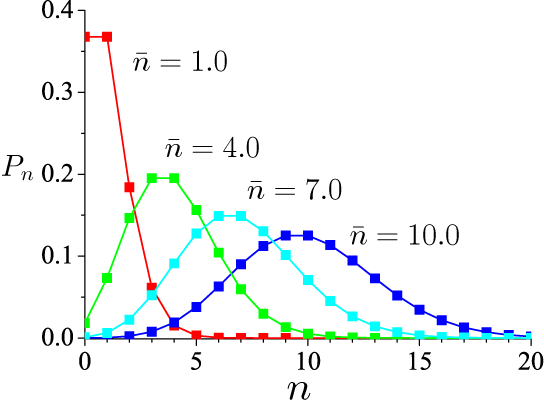
です。式(4)はポアソン分布と呼ばれる離散確率分布の一つで、平均値 bar{n} に対して 個数 n をとる確率分布を表します。 下の図は、式(4)を様々な bar{n} に対してプロットしたものです。

話を元に戻して、コヒーレント状態の空間分布を調べます。 そのために、コヒーレント状態を座標表記で表すため、 |v>と位置演算子の固有ベクトル |x>との内積とります。つまり、式(2)の両辺に左から <x|を掛けると。

(6)

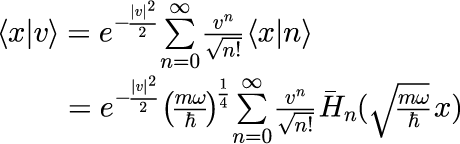
となります。 ただし、１段目から２段目の変形は「１次元量子力学における調和振動子における単一エネルギーの時間発展」の式(12)を用いています。 bar{H}は規格化エルミート多項式です。 式(6)は、複素数 v を与え、和を取ることで具体的に座標依存性を計算することができます。 はじめに、v が実数の場合のコヒーレント状態の空間依存性を計算してみます。

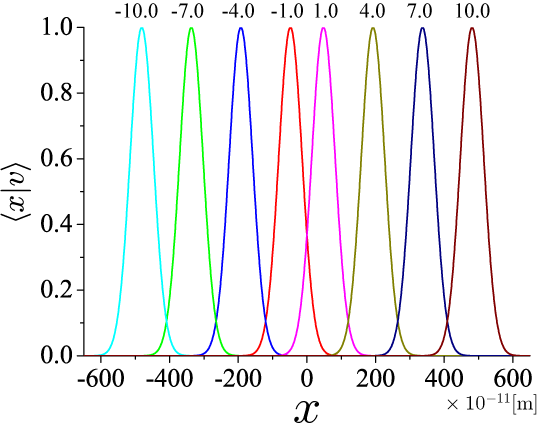
式(6)を用いて数値計算した結果、コヒーレント状態の空間分布は後に示すとおり、ガウス分布となります。中心座標 x_0 は v 大きくなることがわかります。 次に、v が純虚数の場合を計算します。

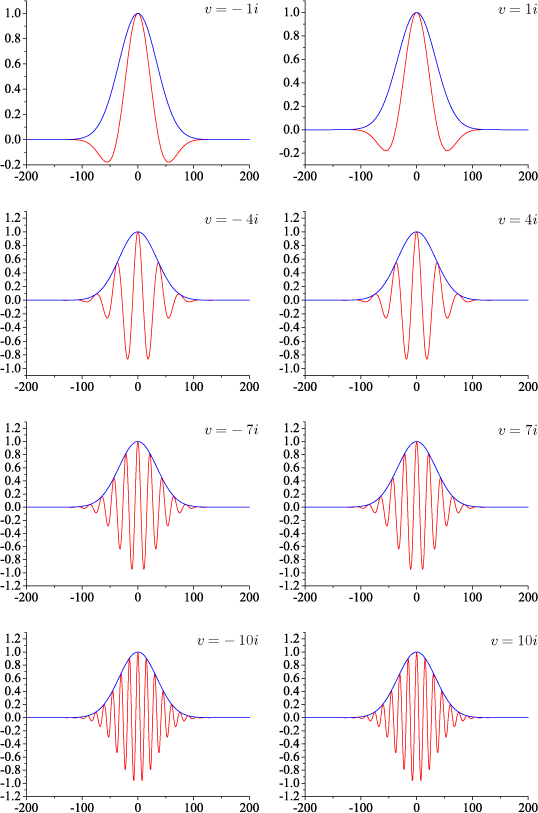
図の赤線はコヒーレント状態の座標表記における実部、青色はコヒーレント状態の座標表記における絶対値です。v が純虚数の場合、中心が x=0 のガウシアンを包絡関数とする波となっていることがわかります。 v が虚数部が大きくなるほど、波数が大きくなっていることがわかります。

上記の２つの図で示した計算結果を、式(6)から解析的に導出します。 エルミート多項式を元の形式に戻して、整理します（参考：「任意の初期状態に対する時間発展」「エルミート多項式の直交性を確かめる」）。

(7)

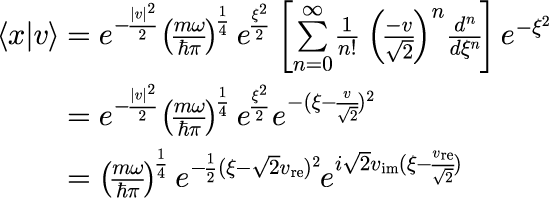
ただし、v_{re} と v_{im} はそれぞれ v の実部と虚部を表し、和は平行移動演算子

(8)

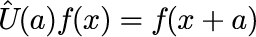
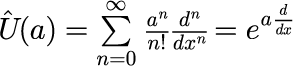
と同じ形をしていることを利用することができます。 式(7)が意味するのは、コヒーレント状態の座標表記はガウシアンで決まる包絡関数と平面波の積で表され、 包絡関数の中心と波数は v の実部と虚部で決まることがわかります。 包絡関数の中心座標は v_{re} = 1 で x_0 = 80.1×10^{-11}[m]となり、半値全幅 Δx = 47.1×10^{-11}[m]となり、上図の数値計算結果と一致します。 ただし、半値全幅は v に依存しません。

次のブラフは、式(6)からコヒーレント状態の空間依存性を v=1(1+i), v=4(1+i), v=7(1+i), v=10(1+i), v=-1(1+i), v=-4(1+i), v=-7(1+i), v=-10(1+i) にて計算した結果をプロットした結果です。

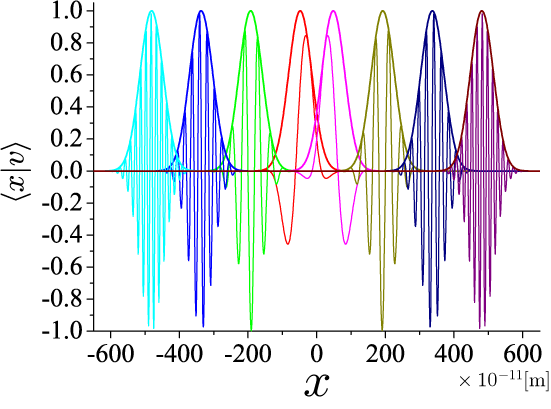
式(7)の解析結果と一致することがわかります。

コヒーレント状態の空間分布の結論

コヒーレント状態の座標表示を用いて空間分布を考えると、コヒーレント状態の空間依存性はガウシアンを包絡関数とする平面波であることを示すことができました。 空間分布の中心座標と平面波の波数は、消滅演算子の固有値 v に依存する一方、 空間分布の半値全幅は v に依存しないことが明らかになりました。