【物理シミュレーションに挑戦！】古典力学
様々な力による物理シミュレーション６：剛体棒で結合された結合力

本項は物理学における様々な系の物理現象を、解析的に扱うのではなく数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・様々な力による物理シミュレーション１：弾性力による運動
・様々な力による物理シミュレーション２：万有引力による運動
・様々な力による物理シミュレーション３：クーロン力による運動
・様々な力による物理シミュレーション４：レナード・ジョーンズ相互作用による運動
・様々な力による物理シミュレーション５：引力＋衝突力
・様々な力による物理シミュレーション６：剛体棒で結合された結合力
・様々な力による物理シミュレーション７：任意の剛体棒で結合された結合力

剛体棒で結合された剛体球

これまでは２点間の距離に応じて生じる力に対する運動の計算アルゴリズムを導出し、シミュレーションを行いました。 本項は、２点間の距離が一定値に固定された２つの剛体球の運動をシミュレーションします。

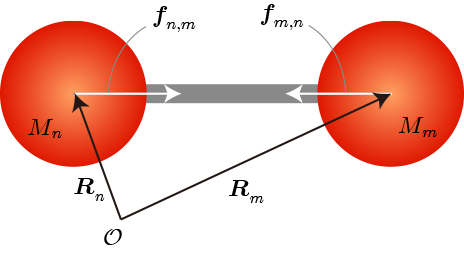
質量０の伸び縮みのしない剛体棒で結合されている２つの剛体球の運動をシミュレーションするための計算アルゴリズムを導出します。２つの剛体球にはそれぞれ結合力が働いていると仮定します。

位置ベクトル、速度ベクトル、加速度ベクトルの条件

２つの剛体球の距離は一定に固定されているため、各々は自由に運動することができません。まず、２つの剛体球の運動が満たすべき関係式を導出します。元となる条件式は「２つの剛体球の距離が一定」

です。この条件式を時間微分することで２つの剛体球の運動に関する条件式を導出することができます。条件式を内積の形

と表しておいて両辺を時刻tで微分します。

これは、速度ベクトルと位置ベクトルが満たすべき関係式です。相対位置ベクトルと相対速度ベクトルは垂直であることを意味しています。さらに時刻tで微分します。

これは加速度ベクトルと速度ベクトル、位置ベクトルが満たすべき関係式です。このように、元の結合条件を時刻で微分することで運動に関する様々な量の関係式を導くことができます。

ニュートンの運動方程式

両剛体球ともニュートンの運動方程式を満たします。

と は結合力を表し、

と表すとします。このように定義することで係数は同符号（ ）、向きは反対（ ）の結合力を表現できます。また、 と は外部から加えられる力を表すとします。この時点では結合力は未知の力です。

２剛体球間の結合力の導出

既知の位置ベクトル、速度ベクトルから未知の結合力を導出します。方針は、運動方程式と条件式を用いて加速度ベクトルを消すことで結合力に関する方程式を導出します。２つの運動方程式の片々を引き算すると、加速度ベクトルを として

となります。この表式と先の条件式から結合力の大きさを決定することができます。

結合された剛体球の運動をシミュレーション

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。