【物理シミュレーションに挑戦！】古典力学
斜面を転がる剛体球運動の計算アルゴリズム１：摩擦力無しの場合

本項は古典力学の様々な系の物理現象を解析的に扱うのではなく、数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・斜面を転がる剛体球運動の計算アルゴリズム１：摩擦力無しの場合
・斜面を転がる剛体球運動の計算アルゴリズム２：摩擦力無しの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム３：静止摩擦力のみの場合
・斜面を転がる剛体球運動の計算アルゴリズム４：静止摩擦力のみの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム５：滑りながら転がる剛体球
・斜面を転がる剛体球運動の計算アルゴリズム６：滑りながら転がる剛体球（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム７：空気抵抗力と転がり摩擦抵抗力
・斜面を転がる剛体球運動の計算アルゴリズム８：斜面との衝突する剛体球（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム９：斜面との衝突する剛体球（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム10：剛体球同士の衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム11：複数剛体球の同時衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム12：接触中の剛体球に衝突した場合（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム13：剛体球同士の衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム14：固定された剛体球に衝突した場合（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム15：力学的エネルギー保存則を満たした斜面との衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム16：力学的エネルギー保存則を満たした剛体球同士の衝突（回転あり）

摩擦力がない斜面に配置された剛体球に加わる力

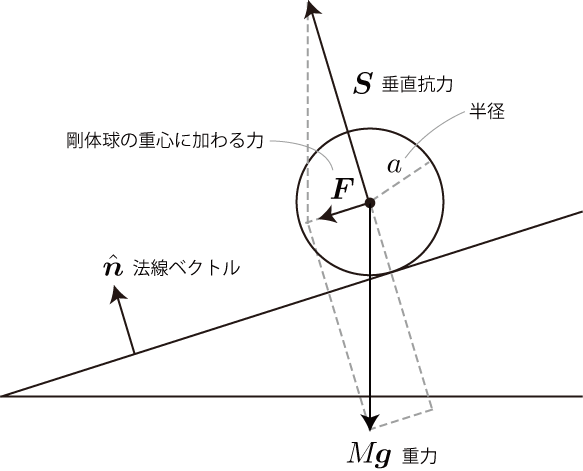
上図で示した質量、 半径の剛体球の運動方程式（重心）は次のとおりです。

ただし、垂直抗力は斜面から受ける力なので、方向は法線ベクトルと必ず一致します。

質量と重力ベクトルが与えられている場合、 この運動方程式を解く上での未知の量はだけです。 次に挙げる運動の制約条件からこのを決定します。

運動の制約条件からの帰着

剛体球が斜面上を滑る場合、剛体球の中心から斜面へ下ろした垂線との交点を\mathbf{R}_0と表した場合、剛体球の重心位置ベクトルは

と表されます。これが運動の制約条件です。さらに、この条件式を時間で微分した

,

も運動の制約条件となります。上記の式は、剛体球の速度ベクトルと加速度ベクトルが斜面の垂直成分を持たないことを意味します。これらの条件を運動方程式に課すことで、未知の垂直抗力Sが決定できます。運動方程式の両辺にとの内積をとると

となり、先の条件を課すと

が得られました。これで運動方程式の未知の量は無くなったので、位置ベクトルについての微分方程式を数値的に解くだけです。

斜面を滑る剛体球のシミュレーション

次の物理シミュレーションは、同じ質量で半径が１[m]と２[m]の剛体球を同じ初速度で運動させた結果です。運動の様子は半径に関係がないことがわかります。また、先に挙げた計算アルゴリズムにて両辺をMで割ることができるため、質量にも依存しません。

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。