【物理シミュレーションに挑戦！】古典力学
斜面を転がる剛体球運動の計算アルゴリズム13：剛体球同士の衝突（回転あり）

本項は古典力学の様々な系の物理現象を解析的に扱うのではなく、数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・斜面を転がる剛体球運動の計算アルゴリズム１：摩擦力無しの場合
・斜面を転がる剛体球運動の計算アルゴリズム２：摩擦力無しの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム３：静止摩擦力のみの場合
・斜面を転がる剛体球運動の計算アルゴリズム４：静止摩擦力のみの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム５：滑りながら転がる剛体球
・斜面を転がる剛体球運動の計算アルゴリズム６：滑りながら転がる剛体球（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム７：空気抵抗力と転がり摩擦抵抗力
・斜面を転がる剛体球運動の計算アルゴリズム８：斜面との衝突する剛体球（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム９：斜面との衝突する剛体球（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム10：剛体球同士の衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム11：複数剛体球の同時衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム12：接触中の剛体球に衝突した場合（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム13：剛体球同士の衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム14：固定された剛体球に衝突した場合（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム15：力学的エネルギー保存則を満たした斜面との衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム16：力学的エネルギー保存則を満たした剛体球同士の衝突（回転あり）

前項では無視した剛体球の回転を考慮した衝突力を示します。回転運動する剛体球同士の衝突の場合、剛体球の接触点で相対的な角速度が減少する方向へ動摩擦力が生じると考えられます。次の図は衝突時に発生する 摩擦力の模式図です。

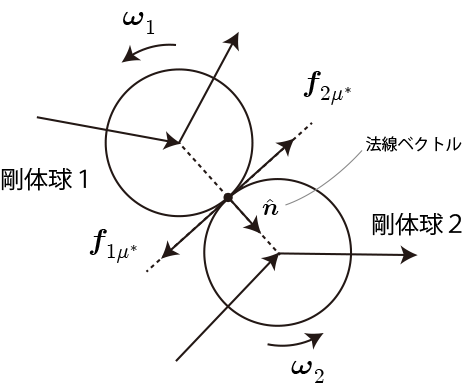
２つの剛体球が衝突する際に生じる摩擦力の向きは両剛体球の回転の角速度に依存します。そこで相対的な角速度を

と定義することにします。「差」ではなく「和」で定義する理由は、衝突時の接触点における摩擦力が０となるのは角速度ベクトルが反転している場合であるためです。つまり、 上記の が有限の値を取る場合に、 の向きに対応した摩擦力が働くと考えることができます。そこで、両剛体球に加わる摩擦力は次のとおりになります。

ただし、 は動摩擦力、 と は前項で示した衝突力です。この摩擦力を重心運動と回転運動に加えることでシミュレーションを行うことができます。

剛体球同士の衝突シミュレーション1

次のグラフィックスは、回転運動する剛体球同士の衝突シミュレーションです。衝突時に回転に応じた重心運動と回転運動が得られていることが確認できました。