【物理シミュレーションに挑戦！】古典力学
斜面を転がる剛体球運動の計算アルゴリズム５：滑りながら転がる剛体球

本項は古典力学の様々な系の物理現象を解析的に扱うのではなく、数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・斜面を転がる剛体球運動の計算アルゴリズム１：摩擦力無しの場合
・斜面を転がる剛体球運動の計算アルゴリズム２：摩擦力無しの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム３：静止摩擦力のみの場合
・斜面を転がる剛体球運動の計算アルゴリズム４：静止摩擦力のみの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム５：滑りながら転がる剛体球
・斜面を転がる剛体球運動の計算アルゴリズム６：滑りながら転がる剛体球（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム７：空気抵抗力と転がり摩擦抵抗力
・斜面を転がる剛体球運動の計算アルゴリズム８：斜面との衝突する剛体球（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム９：斜面との衝突する剛体球（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム10：剛体球同士の衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム11：複数剛体球の同時衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム12：接触中の剛体球に衝突した場合（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム13：剛体球同士の衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム14：固定された剛体球に衝突した場合（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム15：力学的エネルギー保存則を満たした斜面との衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム16：力学的エネルギー保存則を満たした剛体球同士の衝突（回転あり）

静止摩擦力と動摩擦力

「滑る」場合、「滑らずに転がる」場合に続いて、本節では「滑りながら転がる」場合の運動をシミュレーションします。物体と物体がこすれ合う際に発生する摩擦力には、不思議なことに条件に応じて２種類存在します。一つ目は「滑らずに転がる」剛体球に加わる静止摩擦力、２つ目は「滑りながら転がる」剛体球に加わる動摩擦力です。どちらの摩擦力が働くかの条件は次のとおりです。

静止摩擦力が働く条件

条件１：剛体球が接地面で滑っていない（剛体球の回転による接点の軌跡と重心移動距離が一致）
条件２：滑らないために必要な静止摩擦力が最大静止摩擦力よりも小さい

動摩擦力が働く条件

・静止摩擦力の条件を満たさない場合

最大静止摩擦力

いくら剛体球が接地面で滑っていない状態でも最大値があり、最大静止摩擦力と呼ばれます。最大静止摩擦力は接地面に加わる力（垂直抗力）に比例するので、その比例定数を\mu（静止摩擦係数）として

と表されます。ただし、 は接地面の接線方向ベクトルです。滑っていない状態の剛体球が滑らずに転がるために必要な摩擦力がこの最大摩擦力を下回った場合には滑らずに転がるために必要な摩擦力が、上回った場合には最大静止摩擦力が静止摩擦力として剛体球に加わることになります。

動摩擦力

剛体球が接地面で滑っている（回転運動と重心運動が一致しない）場合、剛体球には動摩擦力が加わります。この動摩擦力にも静止摩擦力と同様に最大値が存在します。最大動摩擦力は接地面に加わる力（垂直抗力）に比例するので、その比例定数を （動摩擦係数）として

と表されます。ただし、 は接地面の接線方向ベクトルで、滑りを抑制する方向となります。 なお、動摩擦係数と静止摩擦係数は接触する材質種類ごとによって大きく異なります。ただし、静止摩擦係数の方が動摩擦係数よりも必ず大きくなります。

斜面を滑りながら転がる剛体球の計算アルゴリズム

「摩擦力無しの場合」と「静止摩擦力のみの場合」でシミュレーションした剛体球は、それぞれ動摩擦力が０の状態と、最大静止摩擦力が無限大に対応します。 本項では、斜面を滑りながら転がる剛体球の計算アルゴリズムの導出を行います。

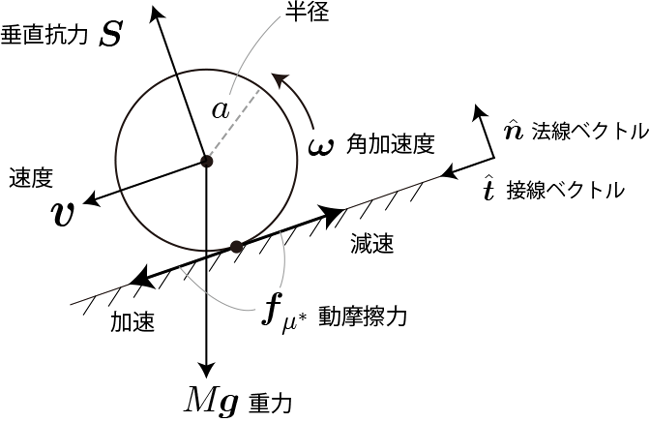
滑りながら転がる剛体球に加わる動摩擦力に関係する力

剛体球が斜面を角速度 で回転しながら速度\mathbf{v}で運動していることを想定します。この状態で摩擦力がどのように働くかを考えます。

静止摩擦力が働く条件と摩擦力

まず、静止摩擦力が働くための条件１を検証するために、回転運動が重心運動と一致しているかを判定する判別式 を定義します。

ただし、 です。もし、回転運動と重心運動が一致していれば となります。ただし、数値計算の場合には厳密に０とはならないので、微小量\deltaを用意して

を満たすときに を満たしていると見なすとします。さらに静止摩擦力が働くための条件２は滑らないで転がるために必要な摩擦力が最大静止摩擦力を下回ることです。両者とも摩擦力の向きは一致するので、絶対値の大小を比較することがわかります。つまり、

を満たす場合に、滑らないで転がるために必要な摩擦力が静止摩擦力として剛体球に加わることになります。

動摩擦力が働く条件と摩擦力

重心運動と回転運動が不一致の場合に剛体球に動摩擦力が働きます。動摩擦力の向きは の逆向きなので、

と表されます。動摩擦力の大きさは一定なので、重心運動と回転運動のズレが小さい場合にそのまま動摩擦力を与えることは不自然です。そのため、本シミュレーションでは、滑らずに回転するために必要な摩擦力がこの動摩擦力よりも大きい場合のみ動摩擦力を与え、小さい場合は滑らずに回転するために必要な摩擦力を与えます。

滑りながら転がる剛体球の計算アルゴリズム

与える摩擦力について

滑らずに回転するために必要な摩擦力

を計算しておきます。重心運動と回転運動が一致している条件、を満たし、 かつの場合には、上記の摩擦力を与えます。また、の場合でも、の場合にも、上記の摩擦力を与えます。それ以外の場合には

斜面を滑りながら転がる剛体球のシミュレーション

次の物理シミュレーションは、斜面に配置した剛体球に、初速度と初期回転を与えた結果です。 初期状態では重心運動と回転運動が一致したいためスピンしながら運動し、途中から一致する様子が確認できます。

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。