【物理シミュレーションに挑戦！】古典力学
斜面を転がる剛体球運動の計算アルゴリズム３：静止摩擦力のみの場合

本項は古典力学の様々な系の物理現象を解析的に扱うのではなく、数値計算による物理シミュレーションを実行するために必要な計算アルゴリズムを示すことを目的とします。 様々な初期条件に対する物理シミュレーションを実現するために、最も汎用的な直交座標系を用います。
・斜面を転がる剛体球運動の計算アルゴリズム１：摩擦力無しの場合
・斜面を転がる剛体球運動の計算アルゴリズム２：摩擦力無しの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム３：静止摩擦力のみの場合
・斜面を転がる剛体球運動の計算アルゴリズム４：静止摩擦力のみの場合の例（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム５：滑りながら転がる剛体球
・斜面を転がる剛体球運動の計算アルゴリズム６：滑りながら転がる剛体球（曲面上の運動）
・斜面を転がる剛体球運動の計算アルゴリズム７：空気抵抗力と転がり摩擦抵抗力
・斜面を転がる剛体球運動の計算アルゴリズム８：斜面との衝突する剛体球（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム９：斜面との衝突する剛体球（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム10：剛体球同士の衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム11：複数剛体球の同時衝突（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム12：接触中の剛体球に衝突した場合（回転なし）
・斜面を転がる剛体球運動の計算アルゴリズム13：剛体球同士の衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム14：固定された剛体球に衝突した場合（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム15：力学的エネルギー保存則を満たした斜面との衝突（回転あり）
・斜面を転がる剛体球運動の計算アルゴリズム16：力学的エネルギー保存則を満たした剛体球同士の衝突（回転あり）

斜面を転がる剛体球の計算アルゴリズム

剛体球が斜面を滑らずに転がる場合の計算アルゴリズムの導出を行います。下図は斜面を転がる剛体球の概念図です。 斜面と剛体球摩擦力が働くことで回転運動が引き起こされると同時に、重心運動にも摩擦力の項が加えられます。

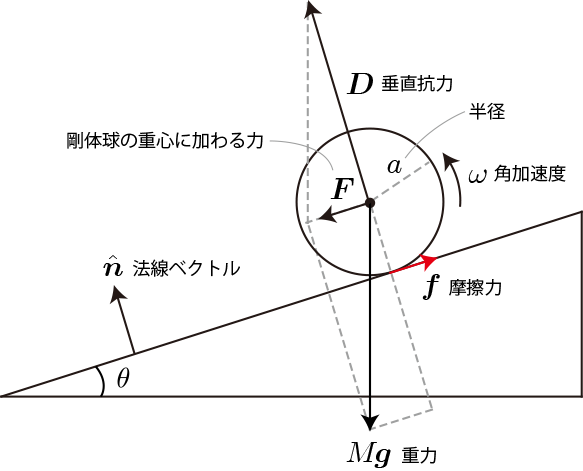
剛体球の慣性モーメントによる回転運動を加えて、運動方程式は次式のように与えられます。

上記の内、垂直抗力と摩擦力が未知の変数です。 この運動方程式に対して運動の制約条件を課すことで計算アルゴリズムの導出を行います。

重心運動の制約条件

剛体球が斜面上を転がる場合、重心位置ベクトルに課せられる条件は滑る場合とは同じです。斜面との接点ベクトルを と表した場合、重心運動に対する制約条件は

,
,
,

と表されます。

回転運動の制約条件

「滑らない」という状況は、球体の回転で移動した距離と球体と斜面との接点の軌跡（円弧）が一致することです。 剛体球の初期状態の重心位置ベクトルと角度ベクトルをそれぞれ 、 とすると、「滑らない」条件は

と表されそうです。しかしながら、上記式は回転方向（回転軸方向）に変化がない場合でのみ成り立つ表式です（もし角度ベクトルの向きが変化した場合、少なくとも位置ベクトルの向きは表式を満たしません）。むしろ、時間で微分した重心の運動速度と回転速度が一致する条件

,

が任意の回転運動で成り立つ制約条件となります。 は角速度ベクトルです。また、さらに両辺を時間で微分した

,

も回転運動に対する制約条件となります。

斜面を転がる剛体球の計算アルゴリズム

重心運動と回転運動に対する制約条件を運動方程式に課すことで、未知の量である 垂直抗力と摩擦力を決定することができます。

この結果を踏まえて、斜面を滑らずに転がる剛体球の計算アルゴリズムは次のとおりです。位置ベクトルと角度ベクトルそれぞれ2階の微分方程式となっていますので、数値的に計算することで運動のシミュレーションを行うことができます。

なお、滑らない場合に働く摩擦力は静止摩擦力と呼ばれます。

斜面を転がる剛体球のシミュレーション

次の物理シミュレーションは、斜面を同じ質量で半径が１[m]と２[m]の剛体球を、同じ初速度で運動させた結果です。 半径が大きいほど全エネルギーの内、回転運動エネルギーに分配される割合が増加することから、重心運動の速度変化は緩慢となります。 なお、転がる場合は質量にも依存することになります。

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。