マクスウェル方程式とシュレディンガー方程式 導入
【0-2】本稿で取り扱う基礎方程式
媒質中のマクスウェル方程式
マクスウェル方程式とは、電磁場の振舞いを記述した方程式で、物理学における基礎方程式の一つとなります。 1864年、当時バラバラに知られていた電磁力に関する法則を整理し、数学的形式を整えることでジェームズ・クラーク・マクスウェルによって導かれました。 組み合わされた電磁力の法則は古い順に、アンペールの法則(1820年)、ファラデーの電磁誘導の法則(1831年)、ガウスの法則(1835年)と、 マクスウェルにより付け足された単磁極の非存在の法則の4つの方程式によって構成されます。
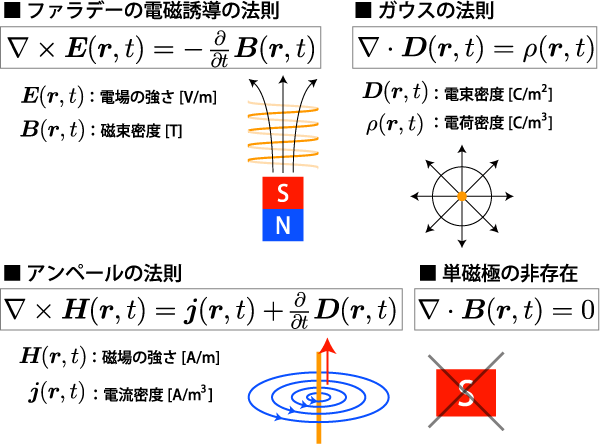
以上の方程式ののうち、電場 E、磁場 H、電束密度 D、磁束密度 B、電流密度 j はベクトル量(本稿ではベクトル量を「ボールド+斜体」で表します)で、電荷密度ρだけがスカラー量です。全ての量は位置 r と時間 t によって変化することが想定されています。 この4つの方程式を組み合わせて問題を解くわけですが、 ファラデーの電磁誘導の法則とアンペールの法則は、(x,y,z)の3成分のベクトル関数の方程式で、ガウスの法則と単磁極の非存在の法則はスカラー関数の方程式なので、それぞれの成分に対する方程式で合計8本の連立方程式となります。
それに対して未知の変数は、電場 E、磁場 H、電束密度 D、磁束密度 B、電流密度 j がそれぞれ3成分と電荷密度ρの1成分を合わせて16個となります。未知の変数よりも方程式の数のほうが少なくて、解くことができません。 そのため実際に問題を解くためには、対象とする物理系に応じて未知の変数を減らしたり、新たな経験則を加えたりすることで、変数と方程式の数を合わせることを行います。
本稿で取り扱う絶縁体は、 自由電荷、電流が存在しないため、

と置くことができます。 また、絶縁体中では電場 E や磁場 H の大きさが小さなうちは、電場 E と電束密度 D、磁場 H と磁束密度 B の間にはそれぞれ比例定数が角振動数ωに依存する比例関係
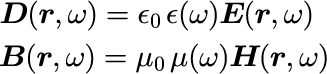
が現象論的に成り立つことが知られています。 つまり、式(2)はマクスウェル方程式の解に対する一種の成立条件となっています。 また、大きな電場や磁場がかかると式(2)からずれることが知られています。 式(2)が成り立たない領域の物理は一般に「非線形光学」と呼ばれます。 もし非線形領域を議論したければ、式(2)右辺の E に関して1次で止めず、2次以降も書きだすことで記述することができます。
式(2)は、角振動数ω一定の世界で成立する方程式です。 時間依存性を議論するためには、角振動数ωの世界から時刻 t の世界をつなぐフーリエ変換
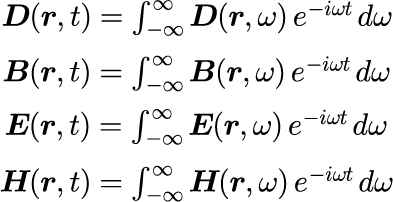
を計算することができます。式(2)の比例係数は誘電率と透磁率とそれぞれ呼ばれます。
以上をまとめると、絶縁体中のマクスウェル方程式は
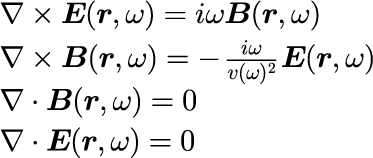
となります。ただし、
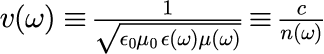
です。 式(5)の n は屈折率と呼ばれ、媒質の電場応答を表す誘電率と磁場応答を表す透磁率の積で決まる量で、 電磁波に対する媒質の性質を表し、物質定数と呼ばれます。 本来、屈折率 n の角振動数ω依存性などの関数型は、媒質を構成する原子の性質で決まるため、量子力学による取り扱いが必要となります。 しなしながら、フォトニック結晶中の電磁波を取り扱う場合、実験的に得られる屈折率を物質定数として扱うだけで十分であることが知られています。 つまり、フォトニック結晶中の電磁波は、与えられた屈折率 n に対してマクスウェル方程式(式(4))を解くことで得ることができます。
式(4)の適用限度について2つ注意点を上げます。1つ目は一様媒質であるという点です。 もし位置によって依存する媒質中の方程式を導出したければ、式(2)の誘電率と透磁率に位置依存性を含めて、式(3)のフーリエ変換をする必要があります。 2つ目は、式(2)で示した線形近似と呼ばれる比例関係です。
式(4)の連立方程式を組み合わせて電場と磁束密度を計算することができるわけですが、 本稿ではベクトルポテンシャル A を導入することで得られる、式(4)と同等な連立方程式
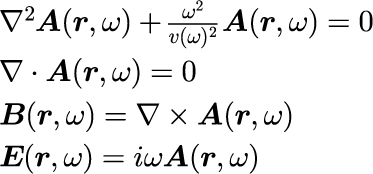
を用います。ベクトルポテンシャルなどを導入してマクスウェル方程式を変形する手法はゲージ変換と呼ばれ、連立方程式の対称性を上げるために一般に行われます。わざわざベクトルポテンシャルなど導入するまでもなく、式(4)から式(6)の第1式と同等の電場(あるいは磁束密度)に対する式を導くことができますが、本稿ではゲージ変換の意味には立ち入らないで、式(6)の形式で進めることにします。
式(6)についてです。 式(6)の第1式は、物理でよく現れるヘルムホルツ方程式と呼ばれる偏微分方程式の型をしています。 ここで注意が必要なのは、ベクトルポテンシャル A はベクトル量である点です。 つまり、A は各位置に対して方向を持った振幅となるわけですが、具体的な量は x,y,z の3成分に関する方程式を連立させて解くことができます。 また、A の方向を制限しているのが第2式です。 これは、A の振幅の向きが電磁波の進行方向に対して直角方向であるということを表しています。 これについては【1-1】一般解の表式で紹介します。
v (あるいは屈折率 n) がスカラー量であるかテンソル量であるかによって複雑さが全く異なります。v がスカラー量であれば3成分は独立して成り立つため、3成分の形式は同等となります。一方、テンソルであれば連立方程式を解く必要があります。一般に、媒質の性質に異方性(入射角や偏光による違い)がある場合にはテンソルとして扱う必要がありますが、 本稿では媒質は等方的であること想定してします。
式(6)の第1式を第2式の条件で得られたベクトルポテンシャルの解を 第3式と第4式にそれぞれ代入することで、電場 E と磁束密度 B が得られるという算段です。 フォトニック結晶中の電磁波の伝搬を考える場合、電場や磁束密度に戻して議論する必要はないので、 本稿ではベクトルポテンシャル A のみで議論します(例外:異なる媒質間の境界条件を課す際)。 最後に、A の時間依存性を計算したければ、フーリエ変換することで得られます。
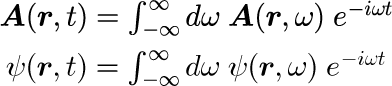
本稿では、式(6)と式(7)を用いてフォトニック結晶中の光パルスの伝搬問題を取り扱います。
シュレディンガー方程式との比較
媒質中のマクスウェル方程式と比較するために、本稿ではポテンシャルが時間に依存しないシュレディンガー方程式を用意します。 式(6)と対応関係にある方程式を示します。
ポテンシャルが時間に依存しない場合
シュレディンガー方程式とは、1926年にエルヴィン・シュレーディンガーによって提案された物質波を表す波動関数の時間発展を記述する、物理学の基礎方程式の一つとして知られます。
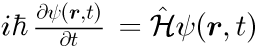
式(7)の H は古典力学との対比からハミルトニアンと呼ばれ、対象とする物理系によってそれぞれ定義されます。 ψは物質波を表す波動関数で、絶対値の2乗がその位置と時刻における存在確率を表すとされています(ボルンの確率解釈)。 最も一般的な H は、ポテンシャルで表すことができる力が物質波に加わっている系で、
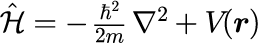
と表されます。 本稿ではポテンシャル V が時間に依存しない場合を考えるため、 式(3)と同様にフーリエ変換することで、時間 t の世界から角振動数ωの世界で成り立つ方程式を導くことができます。
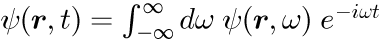
式(8)に式(9),(10)を代入して整理すると、
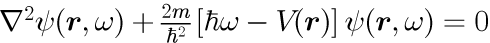
となります。この式は V に位置 r 依存性があるため、式(6)の第1式と同等のヘルムホルツ方程式ではありません。 ヘルムホルツ方程式とするために、位置に依存しない一様ポテンシャルの場合を考えます。
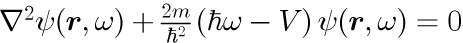
これで式(6)の第1式と同等のヘルムホルツ方程式となり、一様ポテンシャル中の物質波を表す方程式となります。 本稿では、フォトニック結晶中の光パルスの伝搬に対して、井戸型ポテンシャルが周期的に並んだ構造であるクローニッヒ・ペニーモデル中の電子パルスの伝搬について考察を行います。
まとめ
本稿で取り扱う基礎方程式、問題、仮定たち。
一様媒質中のマクスウェル方程式 → フォトニック結晶中の光パルスの伝搬
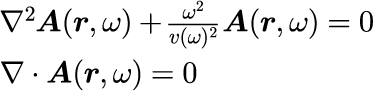
1.線形近似 → 式(2)を仮定
2.一様媒質 → 式(4)が成立しない(誘電率と透磁率に空間依存性を考慮し、ベクトル演算を適切おこなう必要がある。 )
3.等方媒質 → 屈折率 n はスカラー(異方性媒質の場合は n をテンソルにする)
4.吸収なし → 屈折率 n は実数(吸収媒質を議論する際は n に虚数部をもたせる)
一様ポテンシャルのマクスウェル方程式 → クローニッヒ・ペニーモデル中の電子パルスの伝搬
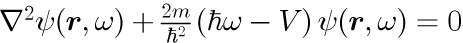
1.ポテンシャルは時間に依存しない → 式(9)を仮定(ポテンシャルが時間に依存する場合、式(11)は成り立たない。)
2.一様ポテンシャル → 式(12)を仮定(ポテンシャル空間依存性がある場合は式(11)を考える必要がある。)
時間依存性はフーリエ変換で計算
最後に、上記のマクスウェル方程式やシュレディンガー方程式の解は位置 r と 角振動数ωに依存する関数となります。 時間発展を得るためには式(3)で定義したフーリエ変換を行うことで計算することができます。
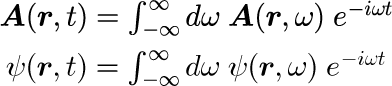
本稿では式(13)を非常に多用することになります。
【目次】シュレディンガー方程式とマクスウェル方程式
- 0.導入
【0-1】はじめに
【0-2】本稿で取り扱う基礎方程式 -
1.一様媒質中における一般解と具体例
【1-1】一般解の表式
【1-2】平面波の時間発展
【1-3】1軸ガウシアンによる光パルスと電子パルス (1軸ガウシアンによる電子パルスの拡散)
【1-4】2軸ガウシアンによる光パルスと電子パルス (2軸ガウシアンによる電子パルスの拡散, 2軸ガウシアンによる光パルスの拡散)
【1-5】3軸ガウシアンによる光パルスと電子パルス
【1-6】垂直1軸ガウシアンによる光ビームと電子ビーム
【1-7】垂直2軸ガウシアンによる光ビームと電子ビーム
【1-8】直線偏光と円偏光
-
2.異なる媒質の境界における電磁波と電子波
【2-1】異なる媒質の境界における波動の一般論
【2-2】電磁波に対する透過係数と反射係数の導出
【2-3】電子波に対する透過係数と反射係数の導出
【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
【2-5】境界面における平面波電磁波の時間発展
【2-6】境界面における平面波電子波の時間発展
【2-7】境界面における1軸ガウシアンによる光パルスと電子パルスの時間発展
【2-8】境界面における2軸ガウシアンによる光パルスと電子パルスの時間発展
【2-9】境界面における3軸ガウシアンによる光パルスと電子パルスの時間発展
【2-10】境界面における垂直1軸ガウシアンによる光ビームと電子ビームの時間発展
【2-11】境界面における垂直2軸ガウシアンによる光ビームと電子ビームの時間発展
-
3.転送行列法
・電子のトンネル確率
・光のトンネル効果
- 4.1層バリアにおける光パルスと電子パルスのシミュレーション
- 5・ポテンシャル障壁による量子粒子のトンネル時間
- 6・フォトニックバンドギャップによる光パルスのトンネル時間
-
7.無限周期構造中の分散関係,群速度,位相速度
・転送行列とブロッホの定理
・ブロッホ波数と透過係数の関係
・分散関係
・透過係数と群速度の関係
-
8.有限サイズの結晶における光パルスと電子パルスの横断時間
・光パルスと電子パルスの横断時間の導出
・パルス伝搬速度と群速度の関係
-
9.フォトニックバンド端における光パルスの遅延
・1次元フォトニック結晶における透過係数と横断時間の数値計算
・横断時間の解析解
-
10.バンド端における電子パルスの遅延
・1次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
・横断時間の解析解
- 11.非周期構造における光パルスと電子パルスと伝搬
































