一様媒質中における一般解と具体例
【1-2】平面波の時間発展
平面波の時間発展の表式
【1-1】一般解の表式で示した一様媒質中のマクスウェル方程式と一様ポテンシャル中のシュレディンガー方程式の一般的表式
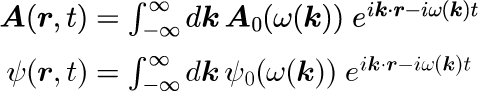
と分散関係
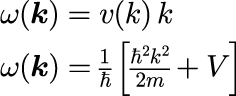
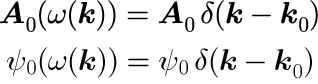
とすることで、式(1)の波数 k による積分のうち特定の波数(k_0)だけを抜き出すことになります。 式(3)を式(1)に代入し積分を実行すると、
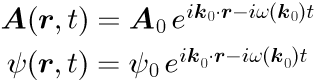
となります。式(4)のk_0は任意です。3次元空間を伝搬する平面波を表す波数は一般的に
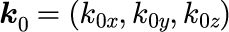
と表すことができます。本節では、平面波の進行方向をz-x平面にとり、平面波の進行方向と z軸とのなす角をθとします。
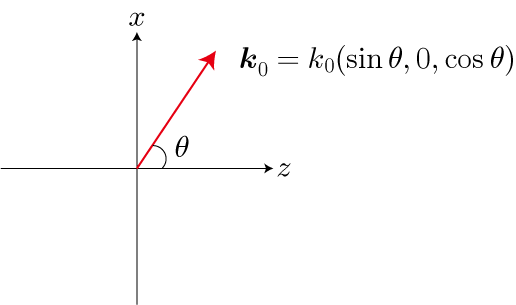
あとは、式(4)を用いて平面波の時間発展を計算する上で必要なパラメータを設定するだけなのですが、 あと1つだけ未知の変数が存在します。それは分散関係(式(2))の v(ω)です。 v(ω)は(0-2-5)で定義したとおり、光速 c を屈折率 n(ω)で割ったもので、媒質中の光の伝搬速度を表します。 一般に n(ω) は光の角振動数ωに依存しますが、n のωに対する変化が少ない領域に限れば、屈折率 n がωに依存しないという近似が成り立ちます。
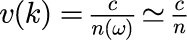
フォトニック結晶中の光の性質を議論する場合この近似がよく使われます。 本稿ではフォトニック結晶における光パルスの伝搬を議論するするため、 以後この近似を暗黙に仮定することにします。 つまり、式(2)の分散関係は
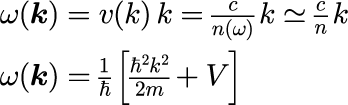
を想定します。
光および電子による平面波の時間発展
式(4)に適切なパラメータを適用することで一様媒質中の光および電子による平面波の時間発展を計算することができます。
光による平面波の時間発展
波数ベクトル k_0 を与えることで、式(4)を用いて平面波の時間発展を計算できるわけですが、適当な値では計算結果が直感的に正しいかどうかの判断が難しくなります。 そのため、計算結果をイメージしやすいパラメータを適切に選んであげる必要があります。 このことは今後複雜な計算を行うほど、計算結果が妥当であるかを判断するために重要度が増していきます。 本節では、光の平面波の時間発展を計算するため、波数ベクトル k_0 を光の波長λ_0を用いて決めることにします。
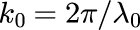
ただし、屈折率 n と波長λ_0は
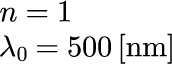
とします。n = 1 は真空中を表し、λ_0 = 500 [nm] は緑色の光を表します。
最後に、ベクトルポテンシャルの振幅 A_0 は(1-1-5)で示したとおり、波数ベクトルの方向、つまり波の進行方向と垂直であれば任意です。
本節では、波の進行方向を z-x平面にとっているので、振幅の向きを y 軸にとることにします。
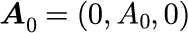
ただし、
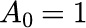
とします。
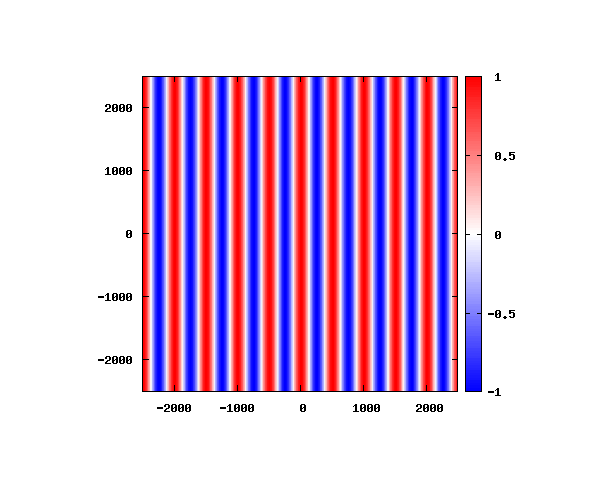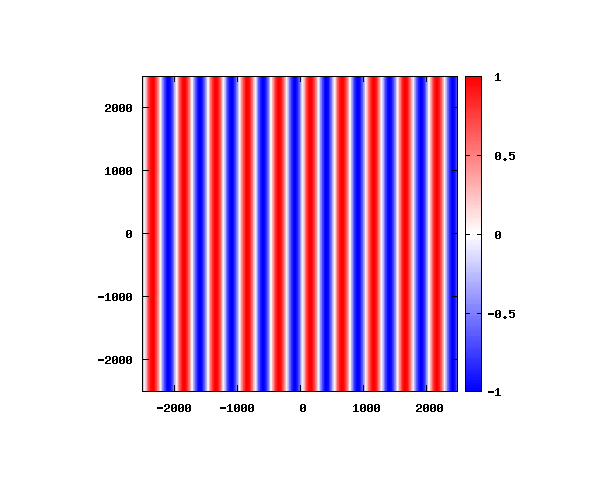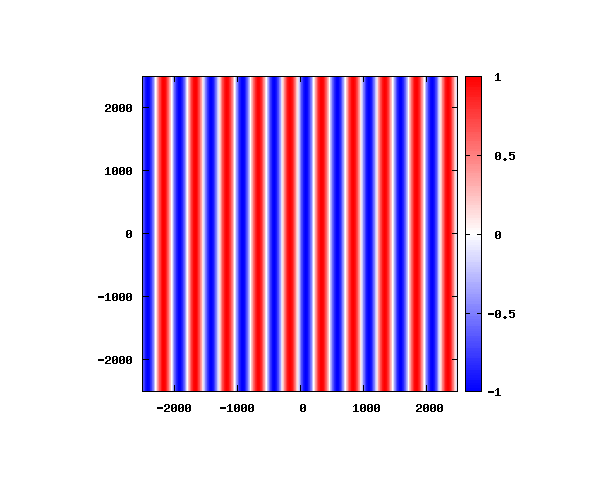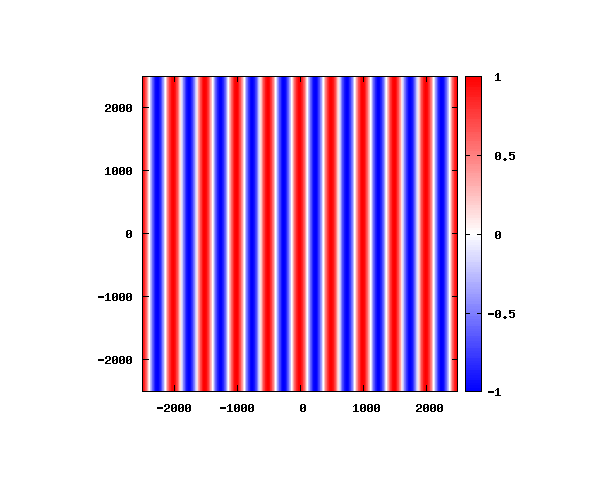
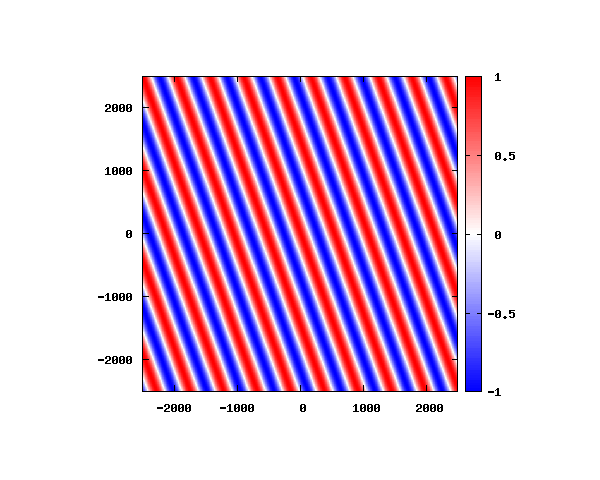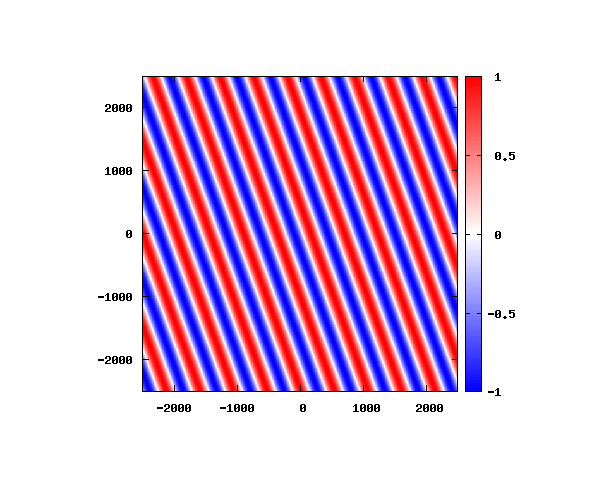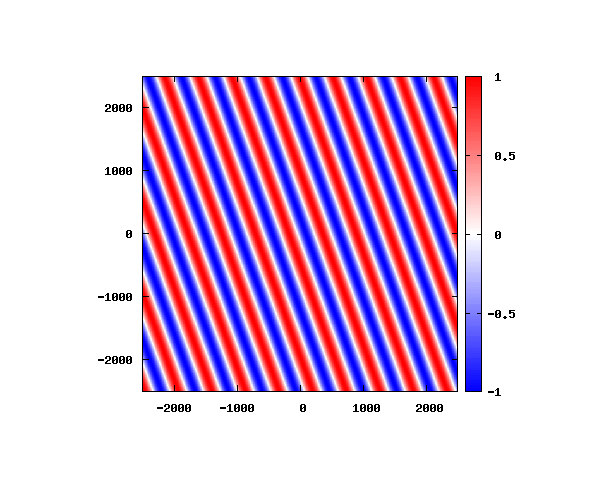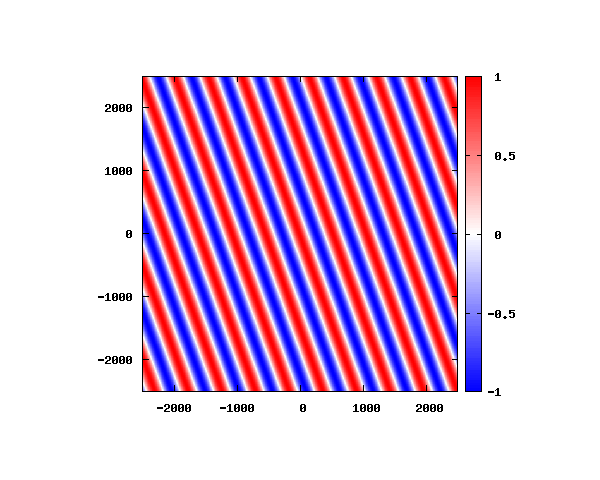
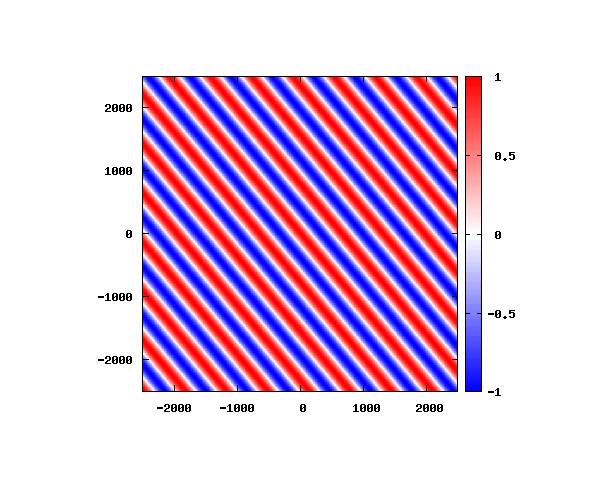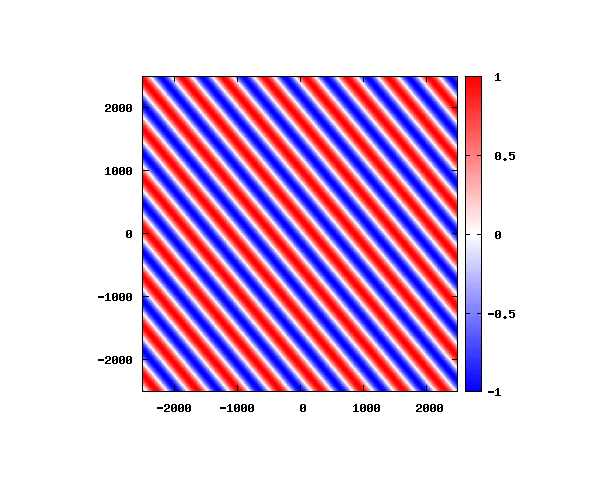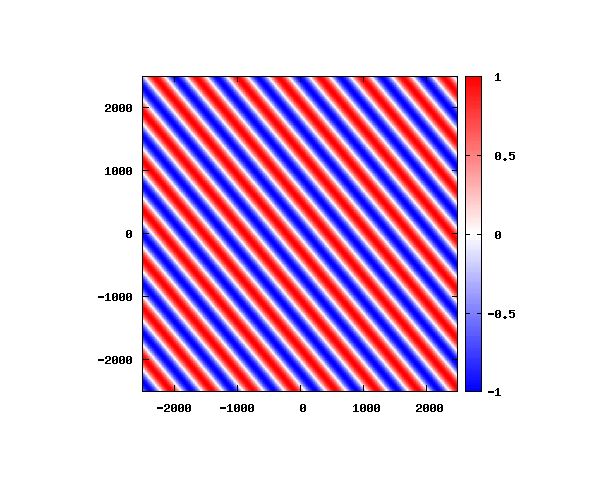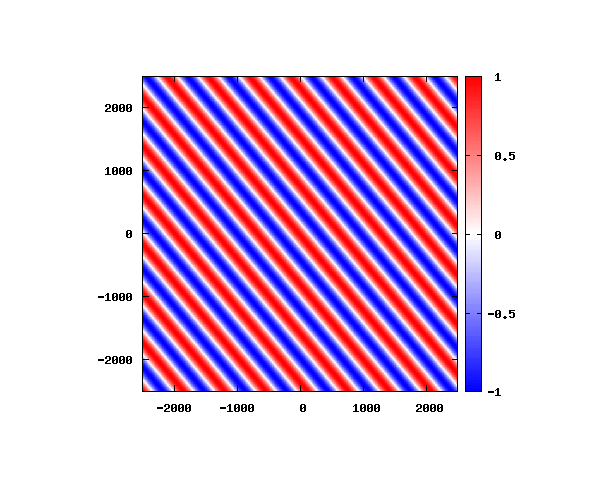
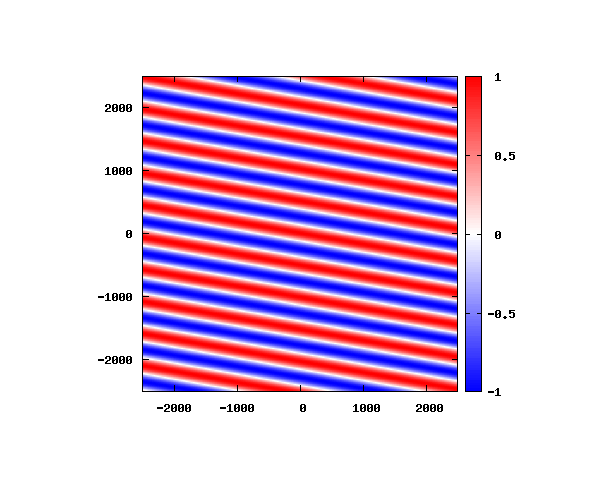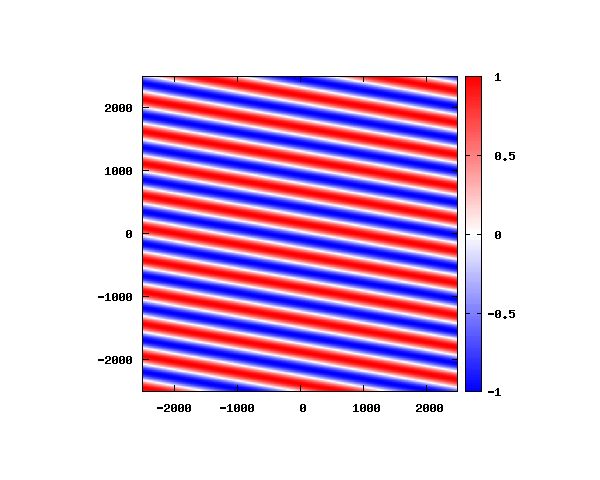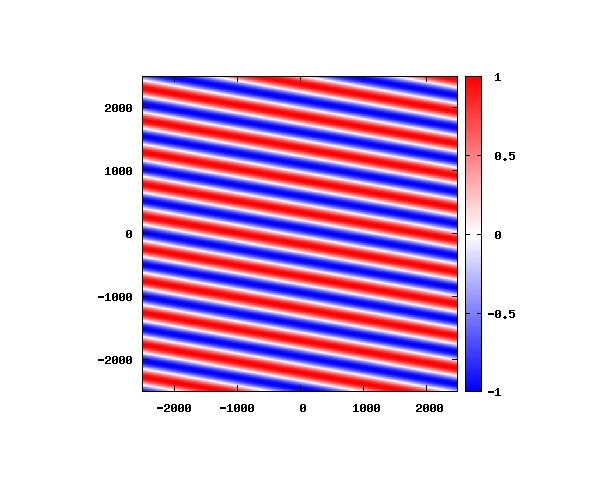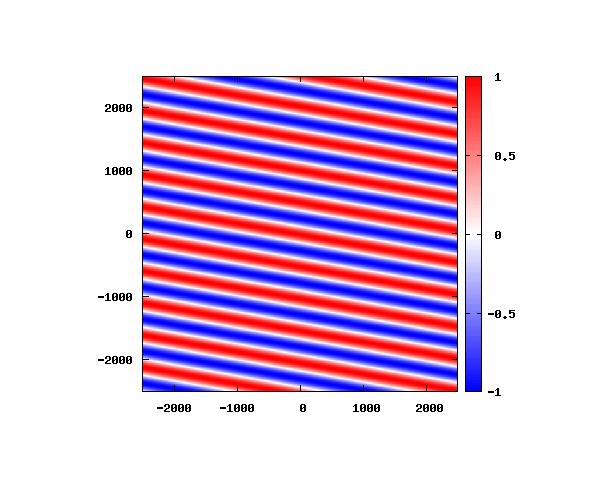
入射角度θ = 0°~ 80°の値で計算した結果を示します。
図のx-y軸のスケールは [nm](10^{-9}[m])となります。
θ=0°
 θ=20°
θ=20°
 θ=40°
θ=40°
 θ=60°
θ=60°
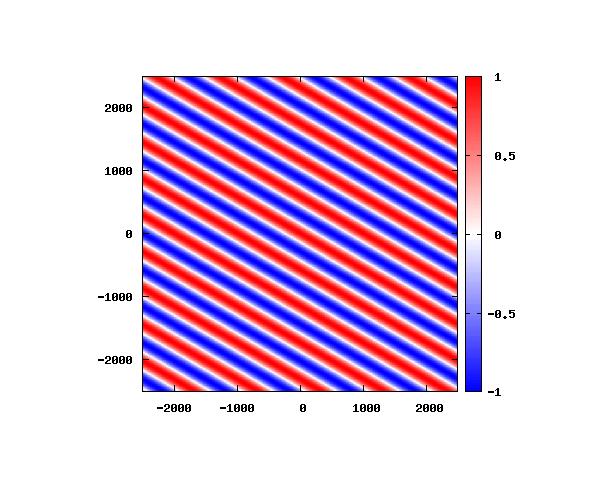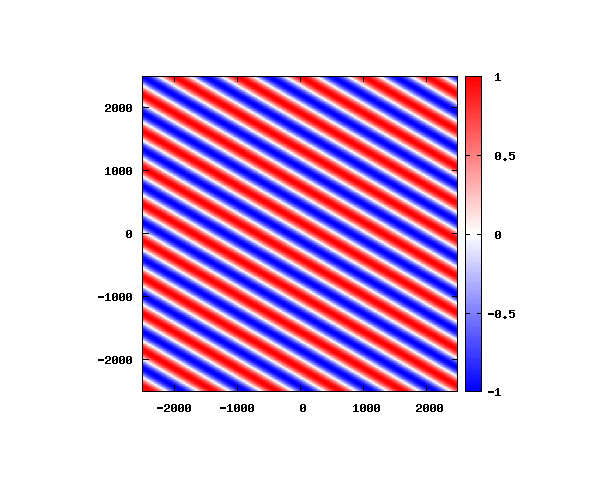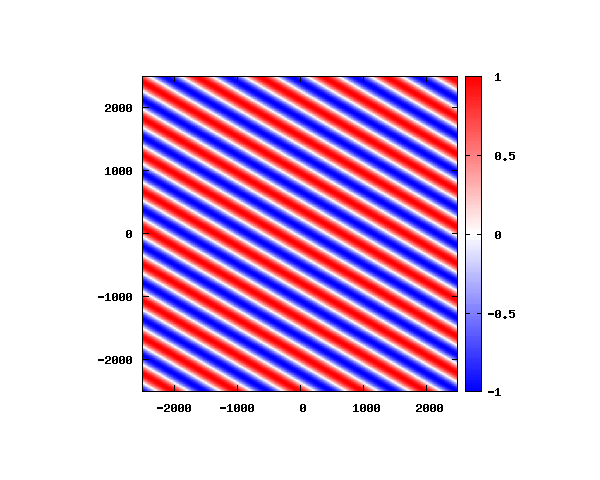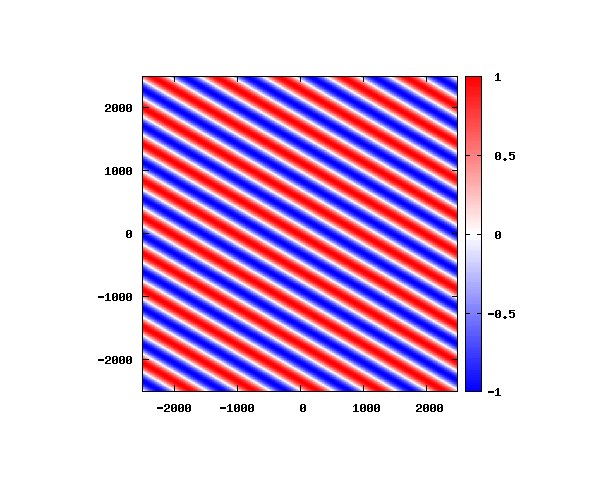 θ=80°
θ=80°
アニメーションの説明
図はベクトルポテンシャルの実部を大きさを色で表しています。赤が 1 で青が -1 です。 マクスウェル方程式では、複素数で表される電場や磁束密度のうち、実部が実際の観測量となります。 つまり、式(0-2-6)を考慮すると、ベクトルポテンシャルの実部は磁束密度となることがわかります。 赤い部分と赤い部分の間隔が 500 [nm] になっていることが確認できます。 また、平面波の場合、時間間隔を適切に取るとアニメーションを無限ループで作ることができます。 その周期は
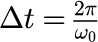
となり、このアニメーションではその周期を1/20にして、20コマの静止画を連続描画して無限ループにしています。 もし時間間隔を上記以外に取ると、アニメーションの最後と最初にて波の位相がずれてしまいます。
電子による平面波の時間発展
同様に電子による平面波の時間発展を式(4)を用いて計算します。 先述の光の波数ベクトル k_0 を与える際には、波長λ_0を基準としましたが、 電子の場合には、波長よりもエネルギー E_0 を基準します。 これは、式(7)の分散関係を波数ベクトル k について解くと
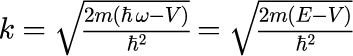
となるためです。式(10)の E は電子のエネルギーを表し
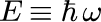
と定義されます。波数ベクトル k の大きさは、エネルギー E とポテンシャル V の差で決まるため、 与えられた V の中での電子の運動を考える場合には、V と同じ次元を持つ E を用いて議論したほうが直感的であることがわかります。 つまり、k_0 を与えるエネルギーを E_0 とすると、
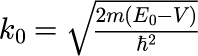
と書くことができます。 本節では、ポテンシャル V と E_0 を
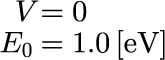
として時間発展を計算し、アニメーション化します。 上記の m は電子の質量で、[eV]はエネルギーの単位をあらわし、それぞれ具体的には

となります。 光の場合と同様、波動関数の振幅は
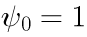
とします。
入射角度θ = 0°~ 80°の値で計算した結果を示します。
図のx-y軸のスケールは [pm](10^{-12}[m])となります。
θ=0°
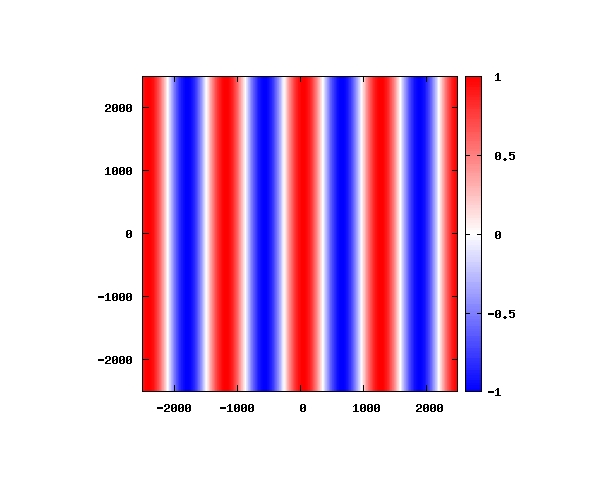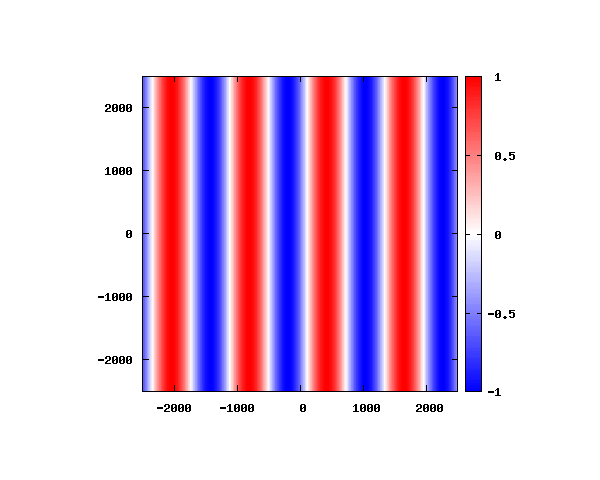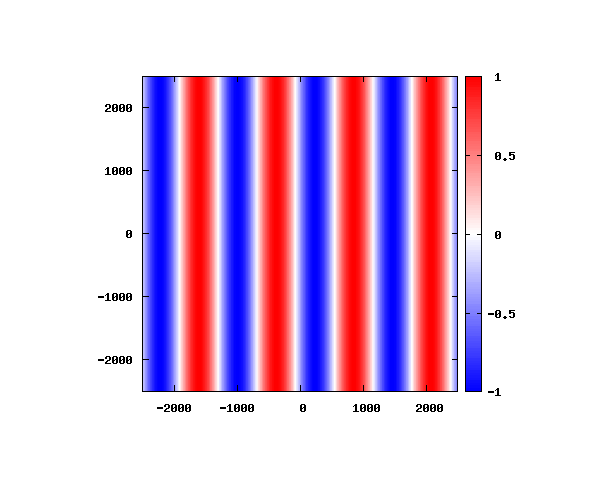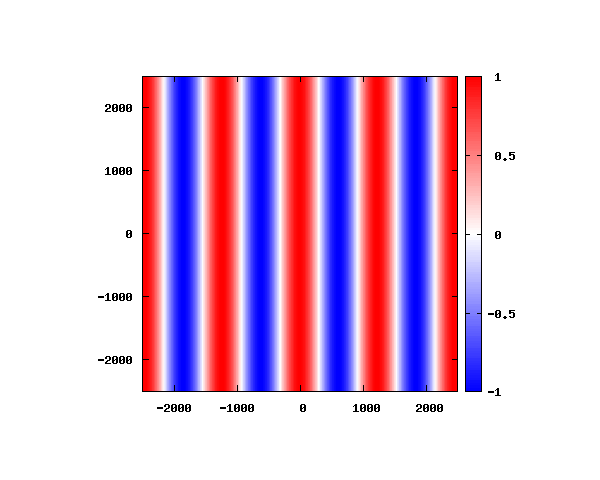 θ=20°
θ=20°
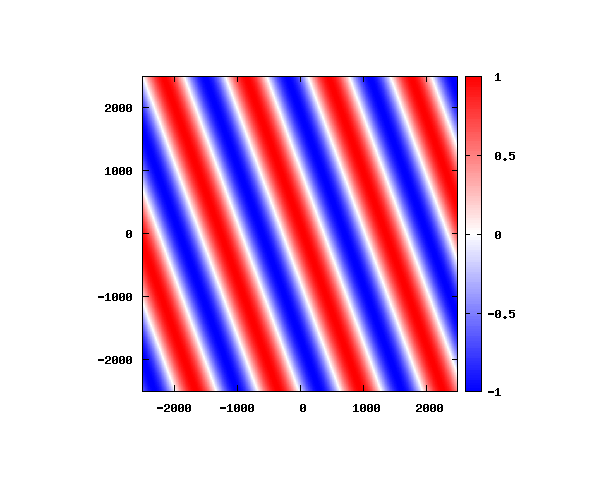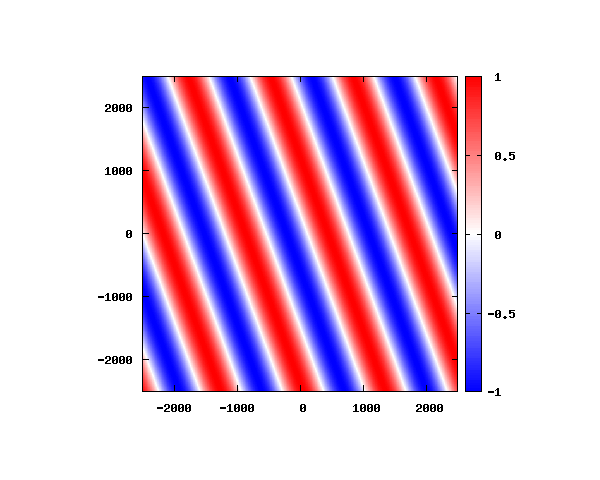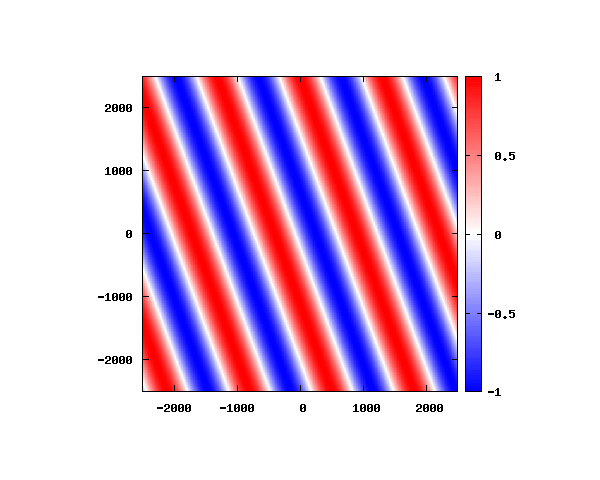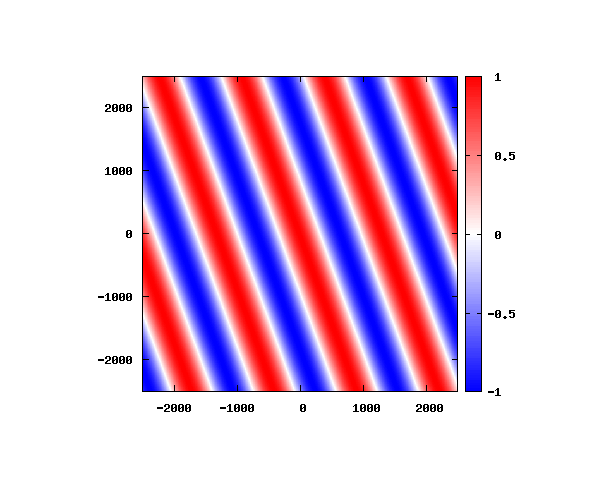 θ=40°
θ=40°
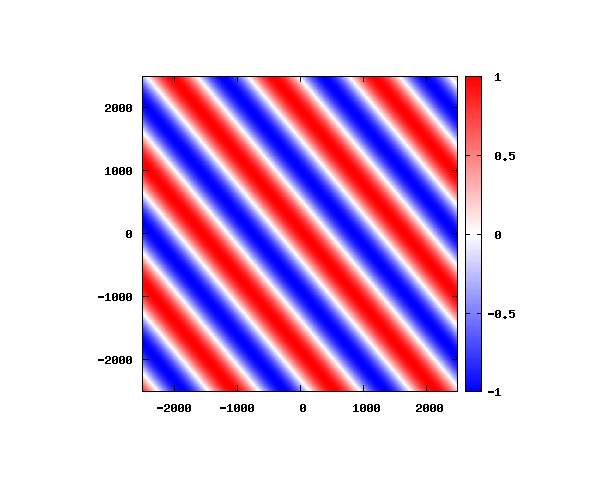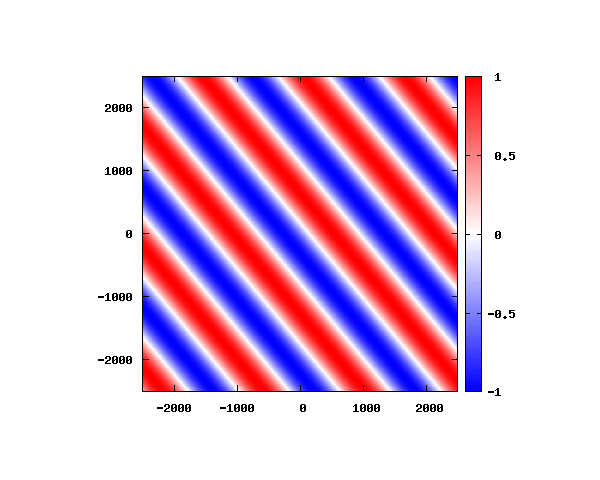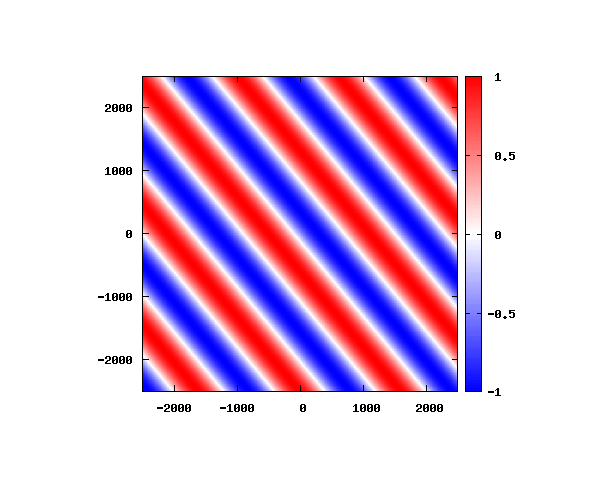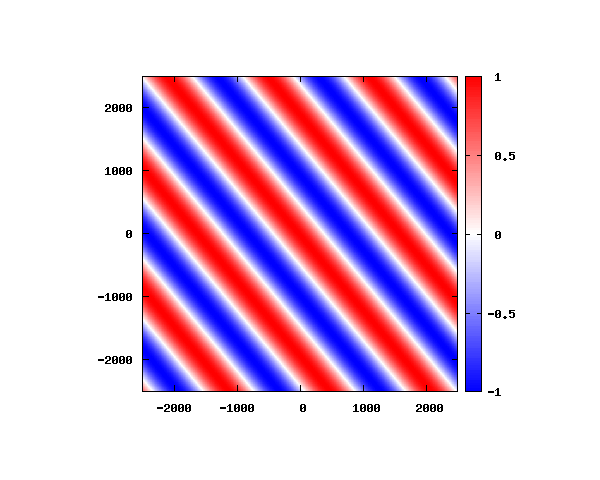 θ=60°
θ=60°
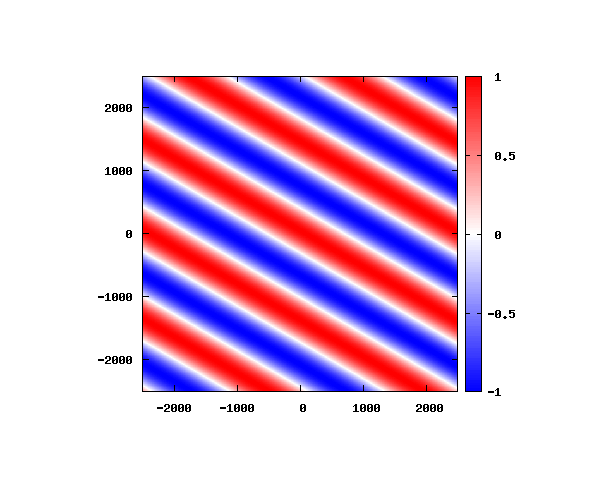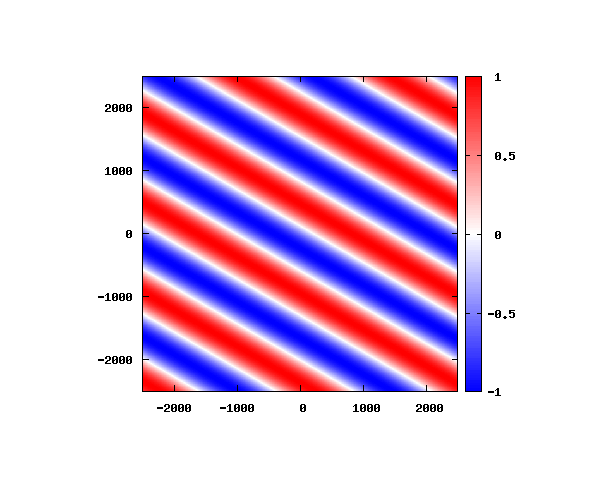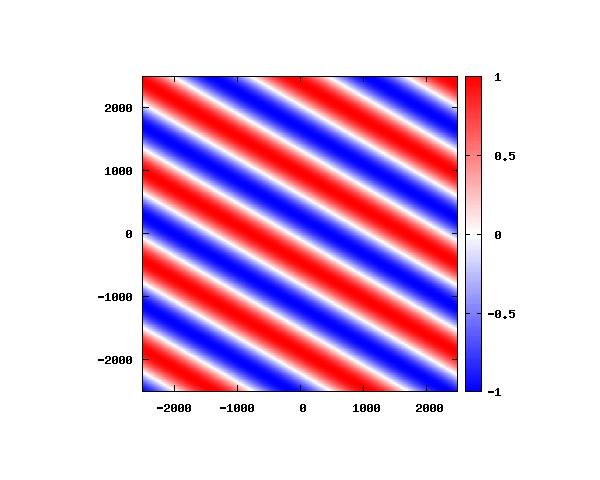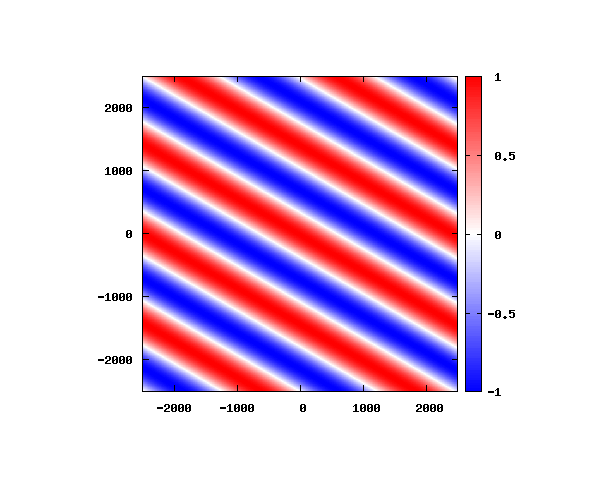 θ=80°
θ=80°
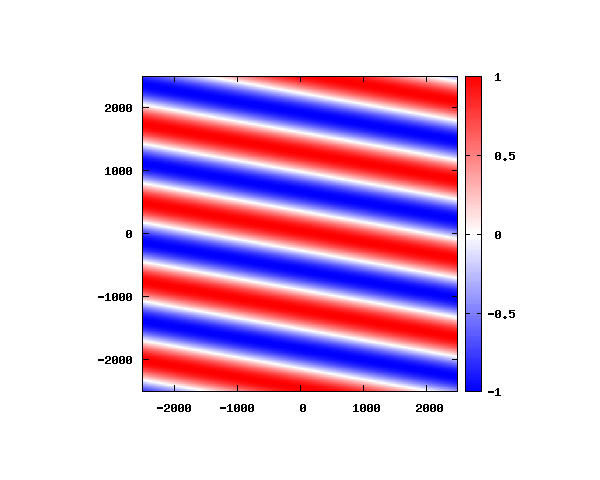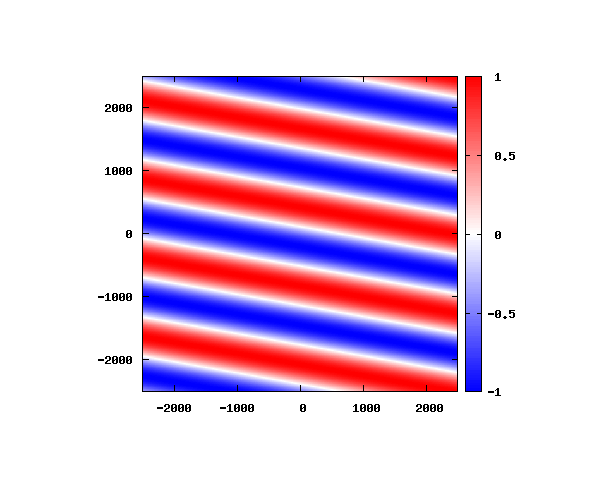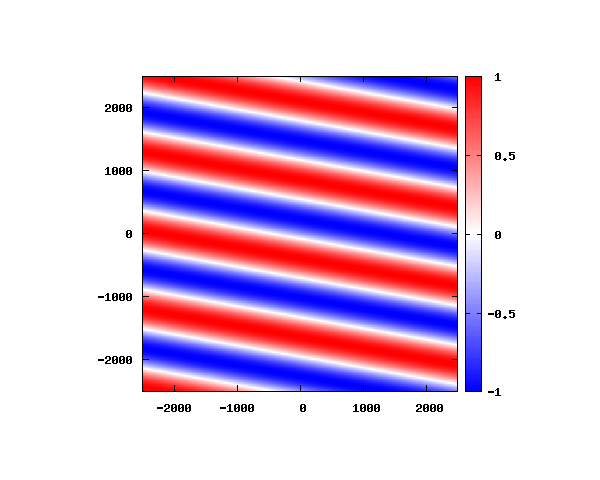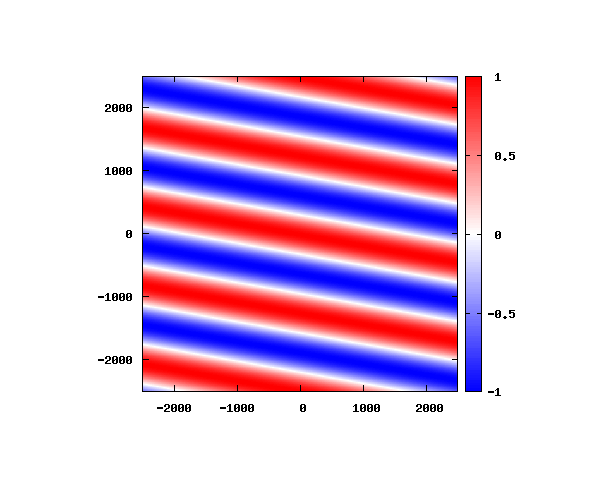
アニメーションの説明
図は波動関数の実部の大きさを色で表しています。赤が 1 で青が -1 です。 光の場合と同様、平面波では時間間隔を適切に取るとアニメーションを無限ループで作ることができます。 量子力学では波動関数の絶対値が観測確率を表す観測量となるため、実部だけを見ることは意味が無いように思えますが、 本節では平面波として計算できているかを確認するため、あえて実部だけを描画しています。 もし絶対値を描画すると次のようになります。
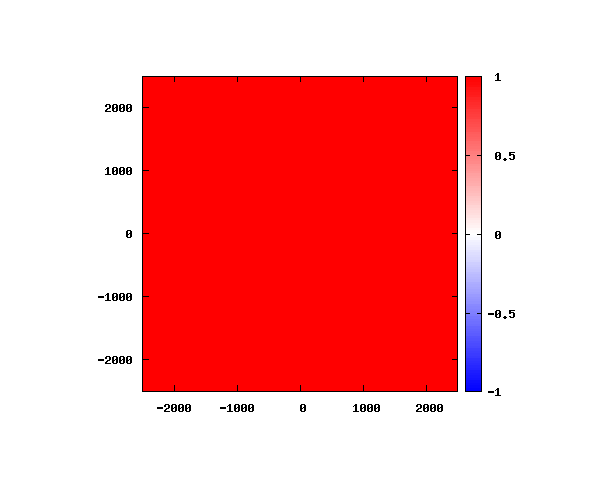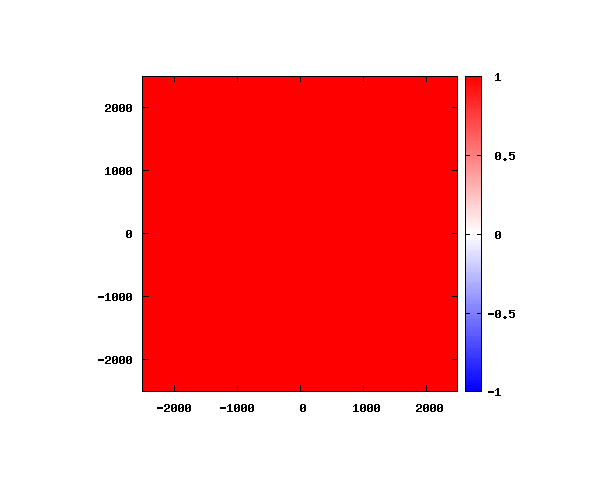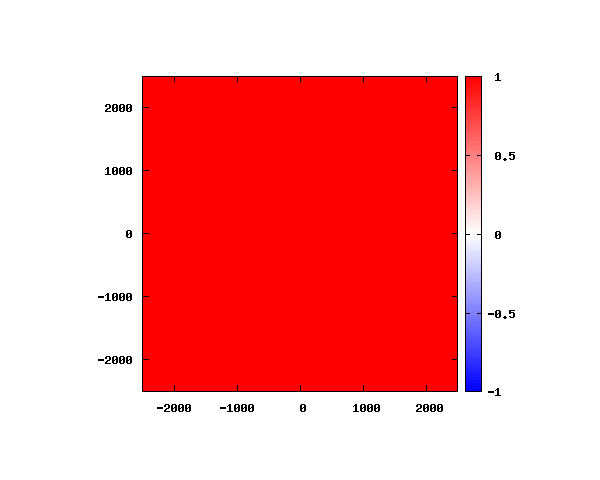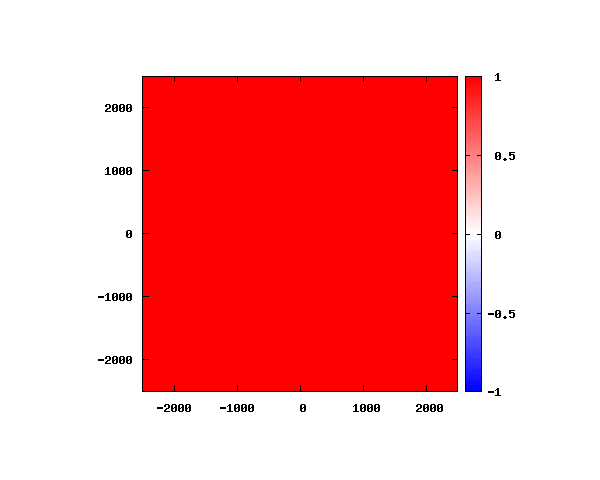
式(4)からも分かる通り、波動関数の絶対値は全空間で1となります。
C++プログラムソース
一様媒質中の光および電子による平面波の時間発展を数値計算するプログラムソースを公開します。
注意点:OpenMPを利用した並列化
本稿では、昨今のCPUの並列化に伴い数値計算も可能な限り並列計算を意識したプログラミングをおこないます。 VisualC++やg++で利用できるOpenMPを利用してC++プログラムの並列化を行い、「#pragma」を利用することでOpenMPが利用できない環境でもソースの変更を行わなくてもよいようにします。本計算では各時刻が独立であるので、CPUに複数のコアがある場合では並列化の恩恵が大きくなるため、積極的に並列化を行います。 並列化プログラミングで非常に重要なのは変数のスコープです。スコープとは変数の有効範囲を表し、変数宣言の位置でその変数の有効範囲が決まるわけですが、 もしその変数宣言の位置が不適切であれば、本来独立であってほしい変数が異なるスレッドから読み書きされることにより、予期しない結果となってしまいます。 例えば、並列化を行い各時刻ごとに別のスレッドで波動関数の空間分布を計算する場合、波動関数の振幅を表す変数は各時刻で独立であって欲しいわけですが、 変数宣言が並列化部分の外であれば、その変数はすべてのスレッドからアクセス可能となります。 つまり、独立に扱いたい変数宣言は並列化のあとに記述する必要があります。
参考
ソースファイル
C++
■光の平面波Maxwell_plane1.cpp
■電子の平面波Schrodinger_plane1.cpp
VisualC++のプロジェクトファイル
■光の平面波Maxwell_plane1.zip
■電子の平面波Schrodinger_plane1.zip
gnuplot テンプレート
【目次】シュレディンガー方程式とマクスウェル方程式
- 0.導入
【0-1】はじめに
【0-2】本稿で取り扱う基礎方程式 -
1.一様媒質中における一般解と具体例
【1-1】一般解の表式
【1-2】平面波の時間発展
【1-3】1軸ガウシアンによる光パルスと電子パルス (1軸ガウシアンによる電子パルスの拡散)
【1-4】2軸ガウシアンによる光パルスと電子パルス (2軸ガウシアンによる電子パルスの拡散, 2軸ガウシアンによる光パルスの拡散)
【1-5】3軸ガウシアンによる光パルスと電子パルス
【1-6】垂直1軸ガウシアンによる光ビームと電子ビーム
【1-7】垂直2軸ガウシアンによる光ビームと電子ビーム
【1-8】直線偏光と円偏光
-
2.異なる媒質の境界における電磁波と電子波
【2-1】異なる媒質の境界における波動の一般論
【2-2】電磁波に対する透過係数と反射係数の導出
【2-3】電子波に対する透過係数と反射係数の導出
【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
【2-5】境界面における平面波電磁波の時間発展
【2-6】境界面における平面波電子波の時間発展
【2-7】境界面における1軸ガウシアンによる光パルスと電子パルスの時間発展
【2-8】境界面における2軸ガウシアンによる光パルスと電子パルスの時間発展
【2-9】境界面における3軸ガウシアンによる光パルスと電子パルスの時間発展
【2-10】境界面における垂直1軸ガウシアンによる光ビームと電子ビームの時間発展
【2-11】境界面における垂直2軸ガウシアンによる光ビームと電子ビームの時間発展
-
3.転送行列法
・電子のトンネル確率
・光のトンネル効果
- 4.1層バリアにおける光パルスと電子パルスのシミュレーション
- 5・ポテンシャル障壁による量子粒子のトンネル時間
- 6・フォトニックバンドギャップによる光パルスのトンネル時間
-
7.無限周期構造中の分散関係,群速度,位相速度
・転送行列とブロッホの定理
・ブロッホ波数と透過係数の関係
・分散関係
・透過係数と群速度の関係
-
8.有限サイズの結晶における光パルスと電子パルスの横断時間
・光パルスと電子パルスの横断時間の導出
・パルス伝搬速度と群速度の関係
-
9.フォトニックバンド端における光パルスの遅延
・1次元フォトニック結晶における透過係数と横断時間の数値計算
・横断時間の解析解
-
10.バンド端における電子パルスの遅延
・1次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
・横断時間の解析解
- 11.非周期構造における光パルスと電子パルスと伝搬
































