一様媒質中における一般解と具体例
【1-1】一般解の表式と平面波

平面波解と分散関係

「【0-2】本稿で取り扱う基礎方程式」で示した基礎方程式からスタートします。

一様媒質中のマクスウェル方程式

(Maxwell)

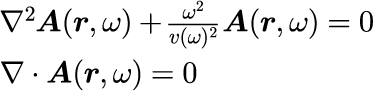
一様ポテンシャル中のシュレディンガー方程式

(Schrodinger)

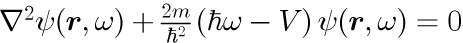
これらの方程式はヘルムホルツ方程式と呼ばれる偏微分方程式の一つの型で、物理でよく登場します。 上記のマクスウェル方程式の v(ω) とシュレディンガー方程式の V が空間的に一様であればこれらの微分方程式は即座に解くことができます。 新しいパラメータの波数ベクトル k

(1-1-1)

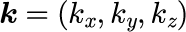
を用いて、

(1-1-2)

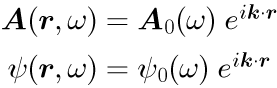
と、ωに依存する任意の係数と指数部分が波数ベクトル k と位置ベクトル r との内積である平面波との積で表されます。 式(1)の波数ベクトル k は波の進む方向と単位長さあたりの波の数を表すベクトル量で、次元は[rad/m]です。 しかしながら、式(2)の k は任意の値をとることが許されているわけではなく、

(1-1-3)

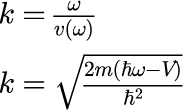
の関係をそれぞれ満たします。 ただし、式(3)の k は式(1)の波数ベクトルの大きさ

(1-1-4)

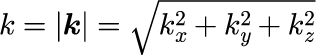
です。 式(3)は式(2)を基礎方程式に代入することで確かめることができます。 波数ベクトル k はωの関数となるわけですが、k とωの関係は分散関係と呼ばれ、 後に詳説する波動の伝播を議論する際に最も重要な概念である位相速度と 群速度と密接な関係があります。 分散関係は名前の通り、時間と共に波が空間的に分散していく様を記述することができますが、後の章で詳説します。 式(2)を見る限り、ベクトルポテンシャル A と波動関数 ψ の２つの解に違いは無いように見えますが、 本稿で示す光パルスと電子パルスの伝播の性質の違いは、つまりは式(3)の分散関係の違いに帰着されることになります。

式(2)の注意点は２つあります。 １つ目は、式(2)は r-ω 空間では平面波であっても、r-t 空間では一般には平面波とはならないことです。 それは、ωの世界から t の世界へとフーリエ変換する際に、係数のω依存性が効いてくるからです。 ２つ目は、ベクトル量であるベクトルポテンシャルの係数の振幅方向と、波の進行方向を決める波数ベクトルの方向は直交することです。 これは電磁波が横波であることを意味します。 このことは、式(2)をマクスウェル方程式の基礎方程式の２つ目に代入することでしめすことができます。

(1-1-5)

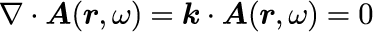
波数ベクトル k とベクトルポテンシャル A の内積が０となることを意味し、つまり２つのベクトルは直交することを意味します。 波の進行方向と直角であれば、ベクトルポテンシャルの振幅の向きは任意であり、まだ自由度が１つ残っています。 この自由度は偏光と呼ばれます。自由空間中の電磁波の場合、進行方向に対して上下左右の区別はないため、偏光の違いは見分けがつきません。 異なる媒質による境界が存在する場合に偏光の違いが現れるため、後の章で詳説することにします。

平面波解の重ね合わせと時間依存性

式(2)の平面波解は式(3)の分散関係さえ満たせば、足し合わせたものも基礎方程式を満たすはずです。 つまり、分散関係を満たしつつ平面波を波数ベクトルに関して積分させた

(1-1-6)

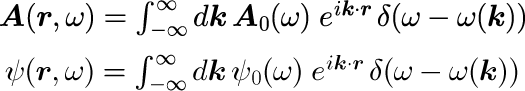
も、元の基礎方程式を満たすことになります。ただし本稿では波数ベクトルの積分表記は

(1-1-7)

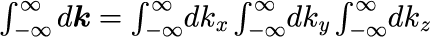
を意味するとします。 さらに、角運動量ωの世界における表式である式(6)は、 式(0-2-13)で示したとおり、フーリエ変換することで任意の時刻 t における解を計算することができます。 つまり、式(6)を式(0-2-13)に代入し、ωの積分を先に実行すると

(1-1-8)

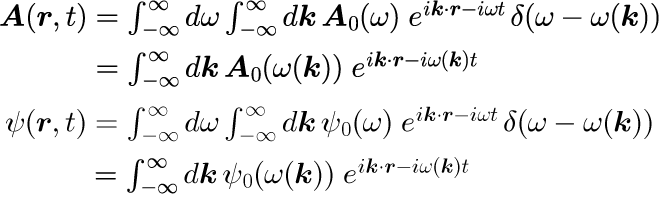
となります。式(8)のω(k)は分散関係（式(3)）を満たす必要がありますが、 それぞれの係数 A_0(ω(k)) や ψ_0(ω(k))のω(k)依存性はまだ任意なので、A_0(ω(k)) や ψ_0(ω(k))の与え方により、任意の時刻 t 、任意の位置 r に任意の形状の波動を創りだすことができるのです。 これは、平面波は完全系を形成できるという事実を利用します。 さらに、式(8)はその任意の形状の波動に対する時間発展を与えているのです。

まとめ

一様媒質中のマクスウェル方程式と一様ポテンシャル中のシュレディンガー方程式の一般的表式は、

(1-1-9)

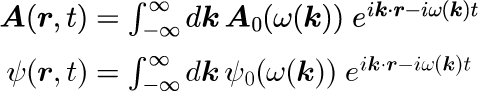
と表すことができます。 式(9)は、係数 A_0(ω(k)) や ψ_0(ω(k))の与え方によって任意の時刻 t 、任意の位置 r に任意の形状の波動を創りだすことができるだけではなく、時間発展も計算することができるのです。 ただし、ω(k)は分散関係

(1-1-10)

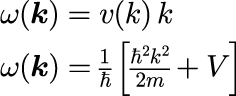
を必ず満たす必要があります。 次節では、係数 A_0(ω(k)) や ψ_0(ω(k))の具体的な与え方と、その計算方法について議論を行います。

【目次】シュレディンガー方程式とマクスウェル方程式

• ０．導入
  　【0-1】はじめに
  　【0-2】本稿で取り扱う基礎方程式
• １．一様媒質中における一般解と具体例
  　【1-1】一般解の表式
  　【1-2】平面波の時間発展
  　【1-3】１軸ガウシアンによる光パルスと電子パルス　（１軸ガウシアンによる電子パルスの拡散）
  　【1-4】２軸ガウシアンによる光パルスと電子パルス　（２軸ガウシアンによる電子パルスの拡散, ２軸ガウシアンによる光パルスの拡散）
  　【1-5】３軸ガウシアンによる光パルスと電子パルス
  　【1-6】垂直１軸ガウシアンによる光ビームと電子ビーム
  　【1-7】垂直２軸ガウシアンによる光ビームと電子ビーム
  　【1-8】直線偏光と円偏光
  
• ２．異なる媒質の境界における電磁波と電子波
  　【2-1】異なる媒質の境界における波動の一般論
  　【2-2】電磁波に対する透過係数と反射係数の導出
  　【2-3】電子波に対する透過係数と反射係数の導出
  　【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
  　【2-5】境界面における平面波電磁波の時間発展
  　【2-6】境界面における平面波電子波の時間発展
  　【2-7】境界面における１軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-8】境界面における２軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-9】境界面における３軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-10】境界面における垂直１軸ガウシアンによる光ビームと電子ビームの時間発展
  　【2-11】境界面における垂直２軸ガウシアンによる光ビームと電子ビームの時間発展
  
• ３．転送行列法
  　・電子のトンネル確率
  　・光のトンネル効果
  
• ４．１層バリアにおける光パルスと電子パルスのシミュレーション
• ５・ポテンシャル障壁による量子粒子のトンネル時間
• ６・フォトニックバンドギャップによる光パルスのトンネル時間
• ７．無限周期構造中の分散関係，群速度，位相速度
  　・転送行列とブロッホの定理
  　・ブロッホ波数と透過係数の関係
  　・分散関係
  　・透過係数と群速度の関係
  
• ８．有限サイズの結晶における光パルスと電子パルスの横断時間
  　・光パルスと電子パルスの横断時間の導出
  　・パルス伝搬速度と群速度の関係
  
• ９．フォトニックバンド端における光パルスの遅延
  　・１次元フォトニック結晶における透過係数と横断時間の数値計算
  　・横断時間の解析解
  
• １０．バンド端における電子パルスの遅延
  　・１次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
  　・横断時間の解析解
  
• １１．非周期構造における光パルスと電子パルスと伝搬