一様媒質中における一般解と具体例
【1-7】垂直２軸ガウシアンによる光ビームと電子ビーム
文責：遠藤 理平 （2011年11月 9日）
カテゴリ：計算物理学(165)
前節「【1-3】１軸ガウシアンによる光パルスと電子パルス」では３種のパルスと２種のビームの定義を行い、その内垂直１軸ガウシアンによる光ビームと電子ビームの時間発展をアニメーション化しました。本節では、垂直２軸ガウシアンによる光パルスと電子パルスについて考えます。
垂直２軸ガウシアンによるビームの表式
係数の与え方
「垂直２軸ガウシアンによるビーム」は、「【1-3】１軸ガウシアンによる光パルスと電子パルス」で定義したとおり、波の進行方向と垂直な２軸に対して空間的に振幅がガウス分布する形状とします。
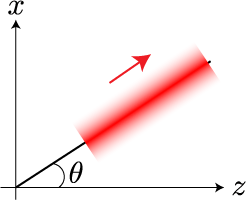
垂直２軸ガウシアンによるビームの定義：、波の進行方向と垂直な２軸に対して空間的に振幅がガウス分布するビーム
このような形状の光ビームと電子ビームは、式(1-3-1)の係数を
(1-7-1)
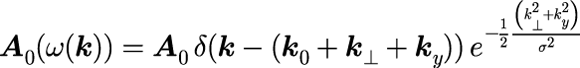
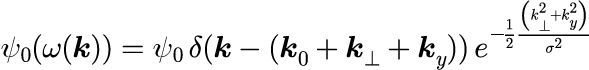
とすることで実現することができます。 光パルスの表式は式(1)を式(1-3-1)に代入し、 波数ベクトルの３成分（k_||, k_⊥, k_y）の積分を計算することで得られます。
(1-7-2)
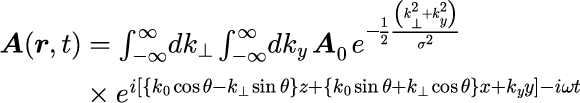
ただし、ωは式(1-3-2)で与えられた分散関係で決まるため、波数ベクトル k は
(1-7-3)
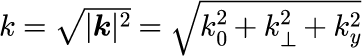
となります。 電子パルスも同様に表すことでき、
(1-7-4)
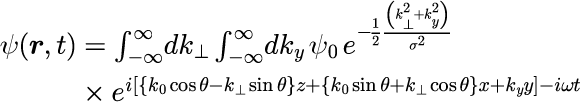
となります。
垂直２軸ガウシアンによる光ビームの計算結果
３次元場の計算には時間がかかるため、本節では時間発展を計算せず、θ=0, t=0 だけを計算することにします。 ３次元場の計算結果は gnuplot では計算することができないので、 OpenGL を用いて３次元プロットすることにします。
プログラムソース
垂直２軸ガウシアンによる光ビームの時間発展を数値計算するプログラムソースを公開します。
C++
■垂直２軸の光ビームMaxwell_beam2.cpp
■３次元密度分布描画プログラム (ver 1.0)OpenGL_3D-1.zip
【目次】シュレディンガー方程式とマクスウェル方程式
- ０．導入
【0-1】はじめに
【0-2】本稿で取り扱う基礎方程式 -
１．一様媒質中における一般解と具体例
【1-1】一般解の表式
【1-2】平面波の時間発展
【1-3】１軸ガウシアンによる光パルスと電子パルス （１軸ガウシアンによる電子パルスの拡散）
【1-4】２軸ガウシアンによる光パルスと電子パルス （２軸ガウシアンによる電子パルスの拡散, ２軸ガウシアンによる光パルスの拡散）
【1-5】３軸ガウシアンによる光パルスと電子パルス
【1-6】垂直１軸ガウシアンによる光ビームと電子ビーム
【1-7】垂直２軸ガウシアンによる光ビームと電子ビーム
【1-8】直線偏光と円偏光
-
２．異なる媒質の境界における電磁波と電子波
【2-1】異なる媒質の境界における波動の一般論
【2-2】電磁波に対する透過係数と反射係数の導出
【2-3】電子波に対する透過係数と反射係数の導出
【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
【2-5】境界面における平面波電磁波の時間発展
【2-6】境界面における平面波電子波の時間発展
【2-7】境界面における１軸ガウシアンによる光パルスと電子パルスの時間発展
【2-8】境界面における２軸ガウシアンによる光パルスと電子パルスの時間発展
【2-9】境界面における３軸ガウシアンによる光パルスと電子パルスの時間発展
【2-10】境界面における垂直１軸ガウシアンによる光ビームと電子ビームの時間発展
【2-11】境界面における垂直２軸ガウシアンによる光ビームと電子ビームの時間発展
-
３．転送行列法
・電子のトンネル確率
・光のトンネル効果
- ４．１層バリアにおける光パルスと電子パルスのシミュレーション
- ５・ポテンシャル障壁による量子粒子のトンネル時間
- ６・フォトニックバンドギャップによる光パルスのトンネル時間
-
７．無限周期構造中の分散関係，群速度，位相速度
・転送行列とブロッホの定理
・ブロッホ波数と透過係数の関係
・分散関係
・透過係数と群速度の関係
-
８．有限サイズの結晶における光パルスと電子パルスの横断時間
・光パルスと電子パルスの横断時間の導出
・パルス伝搬速度と群速度の関係
-
９．フォトニックバンド端における光パルスの遅延
・１次元フォトニック結晶における透過係数と横断時間の数値計算
・横断時間の解析解
-
１０．バンド端における電子パルスの遅延
・１次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
・横断時間の解析解
- １１．非周期構造における光パルスと電子パルスと伝搬
