VisualC++ と OpenGL を利用した仮想物理実験室
【1-2-5】等加速度直線運動のシミュレーション結果と解析解との比較

文責：遠藤理平（2010年8月27日）カテゴリ：仮想物理実験室(325)

【1-1-6】等速度直線運動のシミュレーション結果と解析解との比較と同様に、【1-2-2】等加速度直線運動のシミュレーションでの結果と、【1-2-4】階差数列を用いた等加速度直線運動の解析解の導出で導いた解析解とを比較するためにグラフ化を行います。

VisualC++ の変更

【3.1日目】等加速度直線運動をグラフ化すると同様に、シミュレーションの数値結果をファイルに書き出します。今回はΔt = 1, 0.1, 0.01, 0.01 の４つの場合について、計算結果と解析解との比較を行ないます。また、加速度 a =1[m/s^2]、初速度 v_0 = 0[m/s]、初期位置 x_0 = 0[m] とします。解析解は、式(3.2-8) です。 Δt = 1 のときのファイル名を「ball1.data」、 Δt = 0.1 のときのファイル名を「ball01.data」、 Δt = 0.01 のときのファイル名を「ball001.data」 Δt = 0.001 のときのファイル名を「ball0001.data」とそれぞれの結果を出力するファイル名を変更します。

//////////////////////////////////////////////////////////////////////////
// 変数の定義
//////////////////////////////////////////////////////////////////////////
#define _BITMAP 0 //アニメーション作成用ビットマップの保存 0:しない　1:する
ofstream file1( "ball1.data" ); // <--ここを変更する
//--------------------------------------------------------
// 仮想物理実験室変数の定義
//--------------------------------------------------------
double t = 0.0;  //時刻
double dt= 0.01; //時間刻み // <--ここを変更する
int tn = 0;      //ステップ数

// ボールの定義
struct BALL {
  double x, y, z;
  double vx, vy, vz;
  double ax, ay, az;
};
BALL ball1 = { //初期設定
   0.0, 0.0, 0.0, //(x, y, z)
   0.0, 0.0, 0.0,   //(vx,vy,vz)
   1.0, 0.0, 0.0    //(ax,ay,az)
};

誤差の計算

ファイル出力の３つ目に誤差を書き出すために、「Calculate()」関数を少し変更します。

//--------------------------------------------------------
// 計算と物体の描画
//--------------------------------------------------------
void Calculate(){
  t = dt * double(tn);
  ofs1 << t << " " << ball1.x << " " << <span>abs(ball1.x - 1.0/2.0 * ball1.ax * pow(t,2)) <<endl;

  //位置の算出
  ball1.x = ball1.x + ball1.vx * dt;
  ball1.y = ball1.y + ball1.vy * dt;
  ball1.z = ball1.z + ball1.vz * dt;
  //速度の算出
  ball1.vx = ball1.vx + ball1.ax * dt;
  ball1.vy = ball1.vy + ball1.ay * dt;
  ball1.vz = ball1.vz + ball1.az * dt;

  tn++;
}

t-x グラフとgnuplot のテンプレート：

【3.1日目】等加速度直線運動をグラフ化すると同様に、描画用のテンプレートを用意します。

plot "ball0001.data" using 1:2 linewidth 2 ,\
     "ball001.data" using 1:2 linewidth 2 ,\
     "ball01.data" using 1:2 linewidth 2 ,\
     "ball1.data" using 1:2 linewidth 2
replot

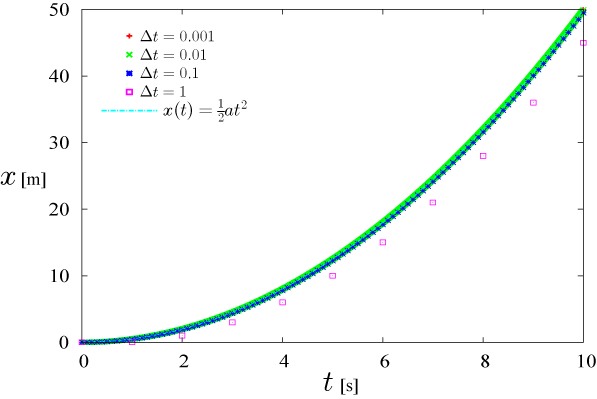
Δt = 1 の場合の解析解とのずれ、すなわち誤差が目立ちます。しかしながらこのグラフでは、どの程度の誤差があるのかがよくわかりません。次に、誤差 |Δx| と t との関係をグラフ化します。

誤差Δx の時間依存グラフとgnuplot のテンプレート：

plot "ball0001.data" using 1:3 linewidth 2 ,\
     "ball001.data" using 1:3 linewidth 2 ,\
     "ball01.data" using 1:3 linewidth 2 ,\
     "ball1.data" using 1:3 linewidth 2
replot

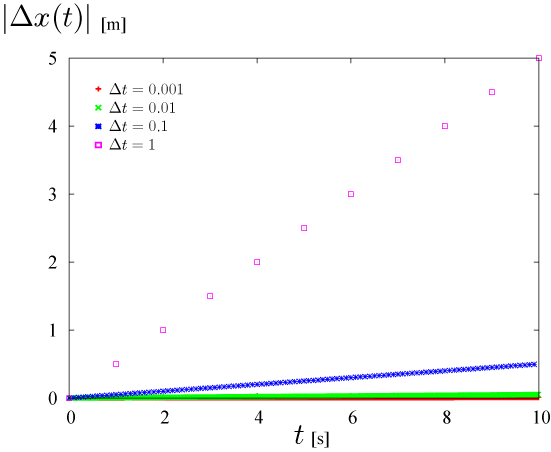
式(3.2-10)のとおり、時刻t の増加とともに、誤差Δx も比例して大きくなることがわかります。。また、Δt が小さいほど、誤差Δx の傾きが小さくなることがわかります。

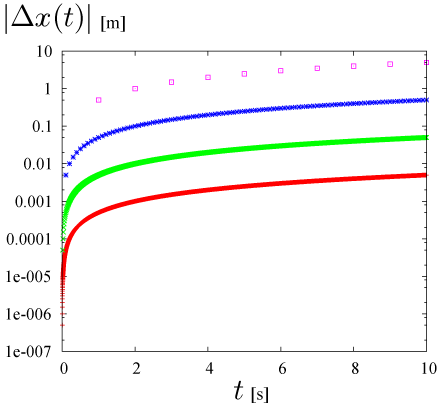
誤差の違いをわかりやすく見るために、誤差|Δx|の軸を対数表示にします。

set logscale y
plot "ball0001.data" using 1:3 linewidth 2 ,\
     "ball001.data" using 1:3 linewidth 2 ,\
     "ball01.data" using 1:3 linewidth 2 ,\
     "ball1.data" using 1:3 linewidth 2
replot