VisualC++ と OpenGL を利用した仮想物理実験室
【2-5-1】重力による斜方投射運動における初速度の分解

【２－４】重力による運動：斜方投射運動では、【2-1-2】重力による運動のアルゴリズムの導出で導出したニュートンの運動方程式を用いて、初期値として x 軸方向の初速度 v_{x0}と z 軸方向の初速度 v_{z0} 設定することで、斜方投射運動をシミュレーション行ないましました。 前回と同じ斜方投射運動のシミュレーションですが、初期値の与え方を変えます。これまでのとおり、【2-1-2】重力による運動のアルゴリズムの導出で導出したニュートンの運動方程式のアルゴリズムからスタートします。

(9.1-1)

斜方放射運動の初期値２

【２－４】重力による運動：斜方投射運動では、v_{z0}を一定として、v_{x0}の値を変化させ場合のシミュレーションを行ないました。v_{z0}と v_{x0}の組み合わせで、初速度 v_0 を計算することができました。

(9.1-2)

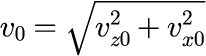
今度は逆に、初速度 v_0 と角度θで運動の初期条件を表現します。多分、多くの人はボールを斜方に投げるとき、z 軸方向の初速度○○、x 軸方向の初速度△△、といったことをイメージしながら投げるということをしていないので、今回の表現のほうが自然ではないでしょうか。

定義：三角比

x-y 平面に長さ１の円を配置し、x 軸方向から y軸方向へ、なす角度θで直線を描きます。 円との交点から x軸と y軸に垂線を下ろします。 そのときの原点0 と垂線と x 軸との交点までの長さを cosθ、 原点と y 軸との交点までの長さを sinθ と表します。

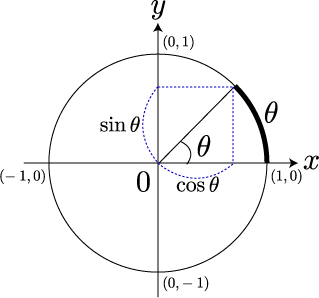
cosθと sinθ は、θの値が変わると変化します。 例えば、
θ=0° → cosθ = 1, sinθ = 0
θ=30°→ cosθ = √3/2 , sinθ = 1/2
θ=45°→ cosθ = 1/√2 , sinθ = 1/√2
θ=60°→ cosθ = 1/2 , sinθ = √3/2
θ=90°→ cosθ = 0 , sinθ = 1
などは、中学生で学習する直角三角形の線分の比と同じで、 三平方の定理で計算することができます。 そのほかのθの場合には暗算できませんが、コンピュータが計算してくれるので心配ありません。

日常生活において、角度の単位は円周を360等分した量で測る度数法（単位：度、記号：°）を用いることが多いです。しかしながら数式で角度を扱う場合、単位円の弧の長さで測る弧度法（単位：ラジアン、記号：rad）と呼ばれるものさしを使います。 半径1 の円周の長さは、2π と小学生で学習します。 例えば、
弧の長さが 2π → θ= 360°
弧の長さが π → θ= 180°
弧の長さが π/2 → θ= 90°
弧の長さが π/3 → θ= 60°
弧の長さが π/4 → θ= 45°
弧の長さが π/6 → θ= 30°
弧の長さが 0 → θ= 0°
と、弧の長さが決まれば、角度θが決まります。 逆の言い方をすれば、弧の長さだけで角度を表すことができるので、 わざわざ度数法の「°」という単位を使う必要がありません。 弧度法では、角度を π[rad]のように指定します。 もともと、πは直径と直径との比という神様が決めた量であるのに対して、 円周を360等分する度数法、たぶん人間が勝手に（歴史的に）決めた量なので、 弧度法のほうがより客観的であることが言えます。 上図の場合、角度がθ[rad]であれば、太線で描いてある弧の長さはθ[m]となります。 （同じθですが、単位が異なります。）

物理量：角度[rad]

(9.1-3)

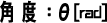
コンピュータプログラミングの際も、この弧度法が利用されています。 とはいえ、度数法もこれまで慣れしてきた分、直感的にイメージしやすいので、今後も利用します。

初速度の設定

以上の三角比を用いて、初速度の z 成分と x 成分とに速度の分解を行ないます。 次の図は、x 軸方向から z 軸方向に角度θ の方向に初速度 v_0 の投射した場合です。

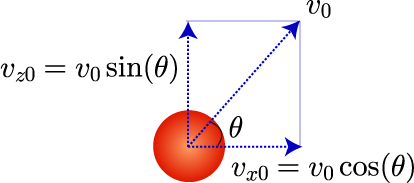
初速度 v_0[m/s]に、cos と sin を掛けたものが、z成分 x成分の初速度となります。 この初速度を用いてシミュレーションを行ないます。

VisualC++ と OpenGL を利用した仮想物理実験室

第０章　仮想物理実験室の構築

• 【０－１】OpenGL と Visual C++ 2008 Express Edition の準備
• 【０－２】仮想物理実験室の構築 ・（0-2-1）ver1.0：基本形 ・（0-2-1）ver1.1：基本形＋ばねの描画 ・（0-2-2）ver1.2：基本形＋ばねの描画
• 【０－３】グラフ作成ソフト gnuplot のインストールと使い方
• 【Ａ－１】参考文献 ・（A-1-1）OpenGL について
  ・（A-1-2）VisualC++ について
  ・（A-1-3）物理シミュレーション
  ・（A-1-4）数値計算
  

第１章　様々な運動

• 【１－１】等速度直線運動
  
  • ・（1-1-1）物理量について
  • ・（1-1-2）等速度直線運動のアルゴリズムの導出
  • ・（1-1-3）等速度直線運動のシミュレーション
  • ・（1-1-4）等速度直線運動のグラフ化
  • ・（1-1-5）等差数列を用いた等速度直線運動の解析解の導出
  • ・（1-1-6）等速度直線運動のシミュレーション結果と解析解との比較
• 【１－２】等加速度直線運動
  
  • ・（1-2-1）等加速度直線運動のアルゴリズムの導出
  • ・（1-2-2）等加速度直線運動のシミュレーション
  • ・（1-2-3）等加速度直線運動のグラフ化
  • ・（1-2-4）階差数列を用いた等加速度直線運動の解析解の導出
  • ・（1-2-5）等加速度直線運動のシミュレーション結果と解析解との比較
  • ・（1-2-6）差分と微分
  • ・（1-2-7）和分と積分
  • ・（1-2-8）微分・積分を利用した等加速度直線運動の解析解の導出
• 【１－３】等加加速度直線運動
  
  • ・（1-3-1）等加加速度直線運動のアルゴリズムの導出
  • ・（1-3-2）等加加速度直線運動のシミュレーション
  • ・（1-3-3）等加加速度直線運動のグラフ化
  • ・（1-3-4）等加加速度直線運動の解析解の導出
  • ・（1-3-5）等速度直線運動のシミュレーション結果と解析解との比較
• 【１－４】等速度円運動
  • ・（1-4-1）等速度円運動のアルゴリズムの導出
  • ・（1-4-2）等速度円運動のシミュレーション
  • ・（1-4-3）等速度円運動のグラフ化
  • ・（1-4-4）等速度円運動の解析解の導出
  • ・（1-4-5）等速度円運動のシミュレーション結果と解析解との比較
• 【１－５】等加速度円運動
  • ・（1-5-1）等加速度円運動のアルゴリズムの導出
  • ・（1-5-2）等加速度円運動のシミュレーション
  • ・（1-5-3）等加速度円運動のグラフ化
  • ・（1-5-4）等加速度円運動の解析解の導出
  • ・（1-5-5）等加速度円運動のシミュレーション結果と解析解との比較

第２章　ニュートンの運動方程式

• 【２－１】重力による運動：自由落下運動
  • ・（2-1-1）加速度・力・質量の関係：ニュートンの運動方程式
  • ・（2-1-2）重力による運動のアルゴリズムの導出
  • ・（2-1-3）重力による自由落下運動のシミュレーション
  • ・（2-1-4）重力による自由落下運動のグラフ化
  • ・（2-1-5）重力による自由落下運動の解析解の導出
  • ・（2-1-6）重力による自由落下運動のシミュレーション結果と解析解との比較
• 【２－２】重力による運動：鉛直投射運動
  • ・（2-2-1）重力による鉛直投射運動のシミュレーション
  • ・（2-2-2）重力による鉛直投射運動のグラフ化
  • ・（2-2-3）重力による鉛直投射運動の解析解
  • ・（2-2-4）重力による鉛直投射運動のシミュレーション結果と解析解との比較
• 【２－３】重力による運動：水平投射運動
  • ・（2-3-1）重力による水平投射運動のシミュレーション
  • ・（2-3-2）重力による水平投射運動のグラフ化
  • ・（2-3-3）重力による水平投射運動の解析解
  • ・（2-3-4）重力による水平投射運動のシミュレーション結果と解析解との比較
• 【２－４】重力による運動：斜方投射運動
  • ・（2-4-1）重力による斜方投射運動のシミュレーション
  • ・（2-4-2）重力による斜方投射運動のグラフ化
  • ・（2-4-2）重力による斜方投射運動の解析解
  • ・（2-4-3）重力による斜方投射運動のシミュレーション結果と解析解との比較
• 【２－５】重力による運動：斜方投射運動２
  • ・（2-5-1）重力による斜方投射運動における初速度の分解
  • ・（2-5-2）重力による斜方投射運動２のシミュレーション
  • ・（2-5-3）重力による斜方投射運動２のグラフ化
  • ・（2-5-4）重力による斜方投射運動２の投射角度と飛距離の関係
  • ・（2-5-5）重力による斜方投射運動２の解析解
  • ・（2-5-6）重力による斜方投射運動２のシミュレーション結果と解析解との比較
• 【２－６】重力＋空気抵抗力による運動：自由落下運動
  • ・（2-6-1）重力＋空気抵抗力による運動の運動方程式とアルゴリズム
  • ・（2-6-2）重力＋空気抵抗力による自由落下運動のシミュレーション
  • ・（2-6-3）重力＋空気抵抗力による自由落下運動の解析解の導出
  • ・（2-6-4）重力＋空気抵抗力による自由落下運動のシミュレーション結果と解析解との比較
• 【２－７】重力＋空気抵抗力による運動：斜方投射運動
  • ・（2-7-1）重力＋空気抵抗力による斜方投射運動のシミュレーション
  • ・（2-7-2）重力＋空気抵抗力による斜方投射運動の解析解の導出
  • ・（2-7-3）重力＋空気抵抗力による斜方投射運動のシミュレーション結果と解析解との比較
• 【２－８】ばね弾性力による運動：単振動運動（１次元）
  • ・（2-8-1）ばね弾性力による運動の運動方程式（１次元）とアルゴリズム
  • ・（2-8-2）ばね弾性力による単振動運動（１次元）のシミュレーション
  • ・（2-8-3）ばね弾性力による単振動運動（１次元）の解析解の導出
  • ・（2-8-4）ばね弾性力による単振動運動（１次元）のシミュレーション結果と解析解との比較
• 【２－９】ばね弾性力による運動：単振動運動（２次元）
  • ・（2-9-1）ばね弾性力による運動の運動方程式と（２次元）アルゴリズム
  • ・（2-9-2）ばね弾性力による単振動運動（２次元）のシミュレーション
  • ・（2-9-3）ばね弾性力による単振動運動（２次元）の解析解：微分・積分を利用した解析解の導出
  • ・（2-9-4）ばね弾性力による単振動運動（２次元）のシミュレーション結果と解析解との比較
• 【２－10】ばね弾性力＋重力がある場合の運動：単振動運動（３次元）
  • ・（2-10-1）ばね弾性力＋重力による運動の運動方程式（３次元）とアルゴリズム
  • ・（2-10-2）ばね弾性力＋重力による単振動運動（３次元）のシミュレーション
  • ・（2-10-3）ばね弾性力＋重力による単振動運動（３次元）の解析解の導出
  • ・（2-10-4）ばね弾性力＋重力による単振動運動（３次元）のシミュレーション結果と解析解との比較
• 【２－11】ばね弾性力＋重力がある場合の運動：多重連結ばねの運動
  • ・（2-11-1）ばね弾性力の一般化
  • ・（2-11-2）ばね弾性力＋重力による多重連結ばねの運動の運動方程式
  • ・（2-11-3）ばね弾性力＋重力による多重連結ばねの運動のアルゴリズムの導出
  • ・（2-11-4）ばね弾性力＋重力による多重連結ばねの運動のシミュレーション
• 【２－12】ばね弾性力＋遠心力がある場合の運動：円運動
  • ・（2-12-1）遠心力の導出
  • ・（2-12-2）遠心力＋ばね弾性力による運動の運動方程式
  • ・（2-12-3）遠心力＋ばね弾性力による運動のアルゴリズムの導出
  • ・（2-12-4）遠心力＋ばね弾性力による運動のシミュレーション
• 【２－13】張力＋重力がある場合の運動：単振子運動.html
  • ・（2-13-1）張力の導出
  • ・（2-13-2）張力＋重力による多重連結ばねの運動の運動方程式
  • ・（2-13-3）張力による多重連結ばねの運動のアルゴリズムの導出
  • ・（2-13-4）張力による多重連結ばねの運動のシミュレーション
• 【２－14】万有引力による運動１：楕円運動
  • ・（2-14-1）万有引力の導出
  • ・（2-14-2）万有引力による運動の運動方程式
  • ・（2-14-3）万有引力による運動のアルゴリズムの導出
  • ・（2-14-4）初速度と軌道の関係
  • ・（2-14-5）万有引力による運動のシミュレーション
• 【２－15】万有引力による運動２：円運動
  • ・（2-15-1）万有引力による運動が円運動になるための条件
  • ・（2-15-2）初速度の与え方
  • ・（2-15-3）万有引力による円運動のシミュレーション
• 【２－16】万有引力による運動３：３体運動
  • ・（2-16-1）３体運動とは
  • ・（2-16-2）万有引力による３体運動の運動方程式
  • ・（2-16-3）万有引力による３体運動のアルゴリズムの導出
  • ・（2-16-3）万有引力による３体運動のシミュレーション

第３章　剛体の運動（エネルギー保存則と運動量保存則）

• 【３－１】床と球の衝突
• 【３－２】壁と球の衝突
• 【３－３】円柱と球の衝突（１次元）
• 【３－４】円柱と球の衝突（２次元 x-y平面）
• 【３－４－２】円柱と球の衝突（２次元 x-z平面）
• 【３－５】球と球の衝突（１次元）
• 【３－６】球と球の衝突（２次元）
• 【３－７】球と球の衝突（３次元）

付録

• 【Ａ－１】参考文献
  ・（A-1-1）OpenGL について
  ・（A-1-2）VisualC++ について
  ・（A-1-3）物理シミュレーション
  ・（A-1-4）数値計算
  

未分類

力学

• ・ ２体問題のシミュレーション（C言語＋ルンゲクッタ法）
• ・ ラグランジュ未定乗数法を用いた２重振子のシミュレーション
• ・ ラグランジュ未定乗数法を用いた球面振子のシミュレーション
• ・ ラグランジュ運動方程式２：極座標を用いた球面振子
• ・ ラグランジュ運動方程式１：極座標を用いた単振子

量子力学

• ・ １次元量子力学の調和振動子における単一エネルギーの時間発展
• ・ １次元量子力学の調和振動子における任意の初期状態に対する時間発展
• ・ １次元量子力学の調和振動子におけるコヒーレント状態の空間分布
• ・ １次元量子力学の調和振動子におけるコヒーレント状態の時間発展
• ・ １次元量子力学の調和振動子における n励起状態の運動量表示
• ・ １次元量子力学の調和振動子における任意の初期運動量分布に対する時間発展
• ・ １次元量子力学の調和振動子における任意の初期運動量分布＋任意の中心座標に対する時間発展
• ・ １次元量子力学の調和振動子における任意の初期空間分布＋任意の中心運動量に対する時間発展（最も簡単な方法）
• ・ 無限に深い２次元井戸型ポテンシャル
• ・ 無限に深い２次元井戸型ポテンシャル２
• ・ 無限に深い２次元井戸型ポテンシャル３
• ・ 無限に深い２次元井戸型ポテンシャル
• ・ ２次元自由粒子
• ・ 無限に深い井戸型ポテンシャルの時間発展２
• ・ シュレディンガー方程式に従う粒子の時間発展２：無限に深い井戸型ポテンシャルの時間発展
• ・ シュレディンガー方程式に従う粒子の時間発展：自由粒子

波動論

• ・ google API を用いてルジャンドル陪関数を描画する
• ・ ルジャンドル陪関数の漸化式と規格化
• ・ 任意の関数をエルミート多項式で展開する
• ・ エルミート多項式の規格化
• ・ エルミート多項式の直交性を確かめる
• ・ 太鼓の振動の固有振動（第１種ベッセル関数）
• ・ 任意の周期関数をフーリエ変換＋逆フーリエ変換する
• ・ ステップ関数のフーリエ級数展開
• ・ デルタ関数の定義
• ・ フーリエ級数展開２：f=x^2
• ・ フーリエ級数１：f=x
• ・ 波動方程式のテスト