VisualC++ と OpenGL を利用した仮想物理実験室
【2-9-2】ばね弾性力による単振動運動（２次元）のシミュレーション

文責：遠藤理平（2010年8月30日）カテゴリ：仮想物理実験室(325)

前節ばね弾性力による運動の運動方程式と（２次元）アルゴリズムでは、ばねの変位が x-y 平面内の場合における、ばね弾性力の運動方程式の導出と、コンピュータでシミュレーションを行うためのアルゴリズムの導出を行ないました。t=t_n[s]のときの加速度 a_n[m/s^2]は、

(2.9.1)

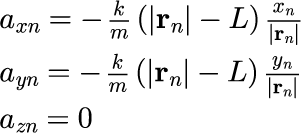
と、そのときのボールの位置 x_n[m/s]によって決まる値となります。 |r_n| とは、原点からボールまでの距離、

(2.9.1)

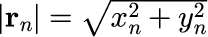
です。コンピュータシミュレーションでは、初期条件として、r_0 = 20.0[m]とし、１０個のボールの質量 m [kg]を変化させて運動の違いを確認します。

ばね弾性力による運動のための計算アルゴリズム

支柱の位置とボールの位置・速度・加速度の初期値

ばね定数を k、自然長 L[m] のばねの片側を固定した動かない支柱を原点に置き、ばねの反対側をボールつけ、x-y 平面上に伸ばします。時刻 t=t_n[s] のときのボールの位置を r_n とします。

k = 10.0;    //ばね定数
L = 30.0;    //ばねの自然長
r = 20.0;    //ボールの初期半径

ball_r = 4.0;//ボールの半径

//支柱の定義
double poll_x = 0.0;
double poll_y = 0.0;
double poll_z = 0.0;
double poll_r = 5.0;  //半径
double poll_h = 20.0; //高さ

速度・位置を逐次計算するアルゴリズム

//位置の計算
x  = x  + vx * dt;
y  = y  + vy * dt;
z  = z  + vz * dt;

r = sqrt(pow(x,2)+pow(y,2));   //<--原点からボールの距離（＝ばねの長さ）

//加速度の計算
ax = - k/m * (r - L) * x/r;    //<-----ばね弾性力からの寄与
ay = - k/m * (r - L) * y/r;    //<-----ばね弾性力からの寄与
az = 0.0;
//速度の計算
vx = vx + ax * dt;
vy = vy + ay * dt;
vz = vz + az * dt;

このアルゴリズムでは誤差が大きく、時間と共に、単振動の振幅が大きくなってしまいます。アルゴリズムの改善は、次に行ないます。

ばね弾性力による単振動のシミュレーション

つるつるの床に、動かない支柱とばねで繋がったボールが運動するシミュレーションです。運動は、ばね弾性力のみによる単振動運動となります。

VisualC++ ＋ OpenGL プログラミング

「【0.2日目】仮想物理実験室の構築（ver1.1）」をベースにプログラミングします。上記で解説した逐次計算を行うアルゴリズムをプログラミングします。

仮想物理実験室変数の定義

//////////////////////////////////////////////////////////////////////////
// 変数の定義
//////////////////////////////////////////////////////////////////////////
#define _BITMAP 1 //アニメーション作成用ビットマップの保存 0:しない　1:する
ofstream ofs1( "ball1.data" );
//--------------------------------------------------------
// 仮想物理実験室変数の定義
//--------------------------------------------------------
double t = 0.0;     //時刻
double dt= 0.01;    //時間刻み
int tn = 0;         //ステップ数
double k = 10.0;    //ばね定数
double L = 30.0;    //ばねの自然長
double r = 20.0;    //ボールの初期半径
double radian; 
double theta;

//支柱の定義
double poll_x = 0.0;
double poll_y = 0.0;
double poll_z = 0.0;
double poll_r = 5.0;  //半径
double poll_h = 20.0; //高さ

// ボールの定義
double ball_r = 4.0;//ボールの半径
struct BALL {
  double m;
  double x, y, z;
  double vx, vy, vz;
  double ax, ay, az;
};
const int N = 10;
BALL ball[N];
void SetUp(void){
  for(int i=0; i<N; i++ ){
    radian = 2.0 * PI * double(i)/double(N);
    ball[i].m  = 2.0*double(i+1)/double(N); //ボールの質量
    ball[i].x  = r * cos(radian);
    ball[i].y  = r * sin(radian);
    ball[i].z  = ball_r; //ボールがめり込まないように
    ball[i].vx = 0.0;
    ball[i].vy = 0.0;
    ball[i].vz = 0.0;
    ball[i].ax = 0.0;
    ball[i].ay = 0.0;
    ball[i].az = 0.0;
  }
}

ボールの位置「x,y,z」、速度「vx,vy,vz」、加速度「ax,ay,az」を構造体「BALL」のメンバとします。「BALL」型の変数「ball1」を宣言と同時に初期値を設定しています。

速度・位置を逐次計算するアルゴリズム

//--------------------------------------------------------
// 計算と物体の描画
//--------------------------------------------------------
void Calculate(){
  t = dt * double(tn);
  //ofs1 << dt*tn << " " << ball1.x << " " << ball1.vx << " " << ball1.ax <<endl;
  for(int i=0; i<N; i++){
    //位置の算出
    ball[i].x = ball[i].x + ball[i].vx * dt;
    ball[i].y = ball[i].y + ball[i].vy * dt;
    ball[i].z = ball[i].z + ball[i].vz * dt;
    r = sqrt(pow(ball[i].x,2)+pow(ball[i].y,2));

    //加速度の算出
    ball[i].ax = - k/ball[i].m * (r - L) * ball[i].x/r;
    ball[i].ay = - k/ball[i].m * (r - L) * ball[i].y/r;
    ball[i].az = 0.0;
    //速度の算出
    ball[i].vx = ball[i].vx + ball[i].ax * dt;
    ball[i].vy = ball[i].vy + ball[i].ay * dt;
    ball[i].vz = ball[i].vz + ball[i].az * dt;
  }
 tn++;
}
void DrawStructure(){
  for(int i=0; i<N; i++){
    glPushMatrix();
      glMaterialfv(GL_FRONT, GL_AMBIENT, ms_silver.ambient);
      glMaterialfv(GL_FRONT, GL_DIFFUSE, ms_silver.diffuse);
      glMaterialfv(GL_FRONT, GL_SPECULAR, ms_silver.specular);
      glMaterialfv(GL_FRONT, GL_SHININESS, &ms_silver.shininess);
      glTranslated(ball[i].x, ball[i].y, ball[i].z); //平行移動値の設定
      glutSolidSphere(ball_r, 20, 20);            //引数：(半径, Z軸まわりの分割数, Z軸に沿った分割数)
    glPopMatrix();
  //バネ
    glPushMatrix();
      glMaterialfv(GL_FRONT, GL_AMBIENT, ms_yellow_rubber.ambient);
      glMaterialfv(GL_FRONT, GL_DIFFUSE, ms_yellow_rubber.diffuse);
      glMaterialfv(GL_FRONT, GL_SPECULAR, ms_yellow_rubber.specular);
      glMaterialfv(GL_FRONT, GL_SHININESS, &ms_yellow_rubber.shininess);  
      drowSolidSpring(box_x, box_y, box_z, (ball[i].x, (ball[i].y,(ball[i].z); //引数：(始点x, 始点y,  始点z, 終点x, 終点y, 終点z )
    glPopMatrix();
  }
  //軸（円錐）
  glPushMatrix();
      glMaterialfv(GL_FRONT, GL_AMBIENT, ms_copper.ambient);
      glMaterialfv(GL_FRONT, GL_DIFFUSE, ms_copper.diffuse);
      glMaterialfv(GL_FRONT, GL_SPECULAR, ms_copper.specular);
      glMaterialfv(GL_FRONT, GL_SHININESS, &ms_copper.shininess);
      glutSolidCone(5.0,20.0,20,20);//引数：(半径, 高さ, Z軸まわりの分割数, Z軸に沿った分割数)
  glPopMatrix();

}

位置「ball1.x」「ball1.y」「ball1.z」
速度「ball1.vx」「ball1.vy」「ball1.vz」
加速度「ball1.ax」「ball1.ay」「ball1.az」
を逐次計算します。先にも述べましたが、このアルゴリズムでは誤差が大きく、時間と共に単振動の振幅が大きくなってしまいます。アルゴリズムの改善は、次回行ないます。